Внесение под дифференциал

Метод подведения под знак дифференциала при интегрировании

Метод, описанный в этой статье, основывается на равенстве ∫ f ( g ( x ) ) d ( g ( x ) ) = F ( g ( x ) ) + C . Его цель – свести подынтегральную функцию к виду f ( g ( x ) ) d ( g ( x ) ) . Для его применения важно иметь под рукой таблицу первообразных и таблицу производных основных элементарных функций, записанную в виде дифференциалов.

Таблица первообразных

d ( C ) = 0 d ( x n ) = n x n — 1 d x d ( ln ( x ) ) = d x x d ( log n x ) = d x x l n ( n ) d ( e x ) = e x d x d ( a x ) = a x ln ( a ) d x

d ( sin x ) = cos x d x d ( cos x ) = — sin x d x d ( t g x ) = d x 1 + x 2 d ( c t g ) — d x sin 2 x

d a r c sin x = d x 1 — x 2 d a r c cos x = — d x 1 — x 2 d a r c t g x = d x 1 — x 2 d a r c t g x = — d x 1 — x 2

Таблица производных основных элементарных функций

∫ x p · d x = x p + 1 p + 1 + C , p ≠ — 1 ∫ 0 · d x = C ∫ a x · d x = a x ln a + C , a ≠ 1 ∫ e x · d x = e x + C ∫ d x x = ln x + C ∫ cos x · d x = sin x + C ∫ sin x · d x = — cos x + C ∫ d x cos 2 x = t g x + C ∫ d x sin 2 x = — c t g x ∫ d x 1 — x 2 = a r c sin x + C ∫ d x 1 + x 2 = a r c t g x + C

∫ d x a 2 + x 2 = 1 a a r c t g x a + C ∫ d x a 2 — x 2 = a r c sin x a + C ∫ d x x 2 — a 2 = 1 2 a ln x — a x + a + C ∫ d x x 2 ± a = ln x + x 2 ± a + C ∫ d x sin x = ln 1 — cos x sin x + C ∫ d x cos x = ln 1 + sin x cos x + C

Найдите неопределенный интеграл ∫ sin ( x 2 ) d ( x 2 ) .

Решение

Мы видим, что в условии подынтегральное выражение уже находится под знаком дифференциала. Согласно таблице первообразных, ∫ sin x d x = — cos x + C , значит, ∫ sin ( x 2 ) d ( x 2 ) = — cos ( x 2 ) + C .

Ответ: ∫ sin ( x 2 ) d ( x 2 ) = — cos ( x 2 ) + C

Найдите множество первообразных функции y = ln 3 x x .

Решение

Для того чтобы найти ответ, нам потребуется вычислить ∫ ln 3 x x d x . Решим задачу с помощью метода подведения под знак дифференциала. Согласно таблице производных, d x x = d ln x , значит, ∫ ln 3 x x d x = ∫ ln 3 x d ( ln x ) . Используя ту же таблицу, можем сразу записать ответ: ∫ ln 3 x x d x = ∫ ln 3 x d ( ln x ) = ln 4 x 4 + C .

Здесь требуется небольшое пояснение. Мы можем ввести еще одну переменную z = ln x и получить ∫ ln 3 x x d x = ∫ ln 3 x d ( ln x ) = ln x = z = ∫ z 3 d z . Тогда, используя таблицу первообразных для степенных функций, можно записать, что ∫ z 3 d z = z 4 4 + C . Теперь вернемся к исходной переменной и получим: z 4 4 + C = z = ln x = ln 4 x 4 + C .

Ответ: ∫ ln 3 x x d x = ln 4 x 4 + C .

С помощью метода подведения под знак дифференциала также можно вычислить первообразные для тангенса и котангенса.

Найдите интеграл тангенса ∫ t g x d x .

Решение

∫ t g x d x = ∫ sin x d x cos x

Поскольку sin x d x = — d ( cos x ) , то можно подвести ∫ sin x d x cos x = — ∫ d ( cos x ) cos x . Берем таблицу первообразных и находим, что — ∫ d ( cos x ) cos x = — ln cos x + C 1 = — ln cos x + C , где C = — C 1 .

Ответ: ∫ t g x d x = — ln cos x + C .

Самым сложным в применении этого метода является определение той части функции, которую нужно подвести под знак дифференциала. Умение быстро делать это приходит с опытом.

Вычислите неопределенный интеграл ∫ x 2 d x 1 + x 6 .

Решение

Согласно таблице производных, d ( x 3 ) = 3 x 2 d x , значит, x 2 d x = 1 3 d ( x 3 ) . Используем таблицу основных интегралов и находим, что ∫ d x 1 + x 2 = a r c r g x + C . Значит, решить задачу методом подведения под знак дифференциала можно так:

∫ x 2 d x 1 + x 6 = ∫ 1 3 d ( x 3 ) 1 + x 3 2 = x 3 = t = = 1 3 ∫ d t 1 + t 2 = 1 3 a r c t g ( t ) + C = x 3 = t = 1 3 a r c t g ( x 3 ) + C

Ответ: ∫ x 2 d x 1 + x 6 = 1 3 a r c t g ( x 3 ) + C

Вычислите неопределенный интеграл ∫ d x x 2 + 2 x + 4 .

Решение

Начнем с преобразования подкоренного выражения.

x 2 + 2 x + 4 = x 2 + 2 x + 1 — 1 + 4 = x 2 + 2 x + 1 + 3 = x + 1 2 + 3

После этого можно записать, что ∫ d x x 2 + 2 x + 4 = ∫ d x x + 1 2 + 3 .

Поскольку d ( x + 1 ) = d x , то ∫ d x x + 1 2 + 3 = ∫ d x ( x + 1 ) x + 1 2 + 3 = x + 1 = z = ∫ d z z 2 + 3 .

Посмотрим в таблицу первообразных и найдем ответ:

∫ d z z 2 + 3 = ln z + z 2 + 3 + C = z = x + 1 = ln x + 1 + ( x + 1 ) 2 + 3 + C = = ln x + 1 + x 2 + 2 x + 4 + C

Ответ: ∫ d x x 2 + 2 x + 4 = ln x + 1 + x 2 + 2 x + 4 + C

Зачастую предварительные преобразования подынтегрального выражения бывают весьма сложными.

Найдите множество первообразных функции ∫ x d x 4 x 2 + 2 x + 1 .

Решение

Начнем также с преобразования выражения под интегралом.

∫ x d x 4 x 2 + 2 x + 1 = ∫ x d x 4 x 2 1 2 x + 1 4 = ∫ x d x 2 x 2 + 1 2 x + 1 4 = = 1 2 ∫ x d x x 2 + 1 2 x + 1 16 — 1 16 + 1 4 = 1 2 ∫ x d x x + 1 4 2 + 3 16

Теперь подведем то, что получилось, под знак дифференциала.

Поскольку d x + 1 4 2 + 3 16 = x + 1 4 2 + 3 16 ‘ d x = 2 · x + 1 4 2 d x = 2 x d x + d x 2 ,то:

2 x d x = d x + 1 4 2 + 3 16 — d x 2 ⇒ x d x = 1 2 d x + 1 4 2 + 3 16 — d x 4

Следовательно, мы можем записать, что:

1 2 ∫ x d x x + 1 4 2 + 3 16 = 1 2 ∫ 1 2 d x + 1 4 2 + 3 16 — d x 4 x + 1 4 2 + 3 16 = = 1 4 ∫ d x + 1 4 2 + 3 16 x + 1 4 2 + 3 16 — 1 8 ∫ d x x + 1 4 2 + 3 16

Исходя из d x = d x + 1 4 , можно преобразовать выражение так:

1 4 ∫ d x + 1 4 2 + 3 16 x + 1 4 2 + 3 16 — 1 8 ∫ d x x + 1 4 2 + 3 16 = = 1 4 ∫ d x + 1 4 2 + 3 16 x + 1 4 2 + 3 16 — 1 8 ∫ d x + 1 4 x + 1 4 2 + 3 16 = = x + 1 4 2 + 3 16 = z x + 1 4 = t = 1 4 ∫ z — 1 2 d z — 1 8 ∫ d t t 2 + 3 16

В итоге у нас получились два интеграла, значения которых можно взять из таблицы.

1 4 ∫ z — 1 2 d z — 1 8 ∫ d t t 2 + 3 16 = 1 4 · 1 — 1 2 + 1 z — 1 2 + 1 — 1 8 ln t + t 2 + 3 16 + C = = 1 2 z 1 2 — 1 8 ln t + t 2 + 3 16 + C = = 1 2 x + 1 4 2 + 3 16 1 2 — 1 8 ln x + 1 4 + x + 1 4 2 + 3 16 + C = = 1 2 x 2 + 1 2 x + 1 4 — 1 8 ln x + 1 4 + x 2 + 1 2 x + 1 4 + C

Ответ: ∫ x d x 4 x 2 + 2 x + 1 = 1 2 x 2 + 1 2 x + 1 4 — 1 8 ln x + 1 4 + x 2 + 1 2 x + 1 4 + C

Метод замены переменной в неопределенном интеграле.
Примеры решений

На данном уроке мы познакомимся с одним из самых важных и наиболее распространенных приемов, который применяется в ходе решения неопределенных интегралов – методом замены переменной. Для успешного освоения материала требуются начальные знания и навыки интегрирования. Если есть ощущение пустого полного чайника в интегральном исчислении, то сначала следует ознакомиться с материалом Неопределенный интеграл. Примеры решений, где я объяснил в доступной форме, что такое интеграл и подробно разобрал базовые примеры для начинающих.

Технически метод замены переменной в неопределенном интеграле реализуется двумя способами:

– Подведение функции под знак дифференциала;
– Собственно замена переменной.

По сути дела, это одно и то же, но оформление решения выглядит по-разному.

Начнем с более простого случая.

Подведение функции под знак дифференциала

На уроке Неопределенный интеграл. Примеры решений мы научились раскрывать дифференциал, напоминаю пример, который я приводил:

То есть, раскрыть дифференциал – это формально почти то же самое, что найти производную.

Найти неопределенный интеграл. Выполнить проверку.

Смотрим на таблицу интегралов и находим похожую формулу: . Но проблема заключается в том, что у нас под синусом не просто буковка «икс», а сложное выражение. Что делать?

Подводим функцию под знак дифференциала:

Раскрывая дифференциал, легко проверить, что:

Фактически и – это запись одного и того же.

Но, тем не менее, остался вопрос, а как мы пришли к мысли, что на первом шаге нужно записать наш интеграл именно так: ? Почему так, а не иначе?

Формула (и все другие табличные формулы) справедливы и применимы НЕ ТОЛЬКО для переменной , но и для любого сложного выражения ЛИШЬ БЫ АРГУМЕНТ ФУНКЦИИ ( – в нашем примере) И ВЫРАЖЕНИЕ ПОД ЗНАКОМ ДИФФЕРЕНЦИАЛА БЫЛИ ОДИНАКОВЫМИ.

Поэтому мысленное рассуждение при решении должно складываться примерно так: «Мне надо решить интеграл . Я посмотрел в таблицу и нашел похожую формулу . Но у меня сложный аргумент и формулой я сразу воспользоваться не могу. Однако если мне удастся получить и под знаком дифференциала, то всё будет нормально. Если я запишу , тогда . Но в исходном интеграле множителя-тройки нет, поэтому, чтобы подынтегральная функция не изменилась, мне надо ее домножить на ». В ходе примерно таких мысленных рассуждений и рождается запись:

Теперь можно пользоваться табличной формулой :

Единственное отличие, у нас не буква «икс», а сложное выражение .

Выполним проверку. Открываем таблицу производных и дифференцируем ответ:

Получена исходная подынтегральная функция, значит, интеграл найден правильно.

Обратите внимание, что в ходе проверки мы использовали правило дифференцирования сложной функции . По сути дела подведение функции под знак дифференциала и – это два взаимно обратных правила.

Найти неопределенный интеграл. Выполнить проверку.

Анализируем подынтегральную функцию. Здесь у нас дробь, причем в знаменателе линейная функция (с «иксом» в первой степени). Смотрим в таблицу интегралов и находим наиболее похожую вещь: .

Подводим функцию под знак дифференциала:

Те, кому трудно сразу сообразить, на какую дробь нужно домножать, могут быстренько на черновике раскрыть дифференциал: . Ага, получается , значит, чтобы ничего не изменилось, мне надо домножить интеграл на .
Далее используем табличную формулу :

Получена исходная подынтегральная функция, значит, интеграл найден правильно.

Найти неопределенный интеграл. Выполнить проверку.

Это пример для самостоятельного решения. Ответ в конце урока.

Найти неопределенный интеграл. Выполнить проверку.

Это пример для самостоятельного решения. Ответ в конце урока.

При определенном опыте решения интегралов, подобные примеры будут казаться лёгкими, и щелкаться как орехи:

В конце данного параграфа хотелось бы еще остановиться на «халявном» случае, когда в линейной функции переменная входит с единичным коэффициентом, например:

Строго говоря, решение должно выглядеть так:

Как видите, подведение функции под знак дифференциала прошло «безболезненно», без всяких домножений. Поэтому на практике таким длинным решением часто пренебрегают и сразу записывают, что . Но будьте готовы при необходимости объяснить преподавателю, как Вы решали! Поскольку интеграла в таблице вообще-то нет.

Метод замены переменной в неопределенном интеграле

Переходим к рассмотрению общего случая – метода замены переменных в неопределенном интеграле.

Найти неопределенный интеграл.

В качестве примера я взял интеграл, который мы рассматривали в самом начале урока. Как мы уже говорили, для решения интеграла нам приглянулась табличная формула , и всё дело хотелось бы свести к ней.

Идея метода замены состоит в том, чтобы сложное выражение (или некоторую функцию) заменить одной буквой.
В данном случае напрашивается:
Вторая по популярности буква для замены – это буква .
В принципе, можно использовать и другие буквы, но мы всё-таки будем придерживаться традиций.

Итак:
Но при замене у нас остаётся ! Наверное, многие догадались, что если осуществляется переход к новой переменной , то в новом интеграле всё должно быть выражено через букву , и дифференциалу там совсем не место.
Следует логичный вывод, что нужно превратить в некоторое выражение, которое зависит только от .

Действие следующее. После того, как мы подобрали замену, в данном примере, , нам нужно найти дифференциал . С дифференциалами, думаю, дружба уже у всех налажена.

После разборок с дифференциалом окончательный результат рекомендую переписать максимально коротко:
Теперь по правилам пропорции выражаем нужный нам :

В итоге:
Таким образом:

А это уже самый что ни на есть табличный интеграл (таблица интегралов, естественно, справедлива и для переменной ).

В заключении осталось провести обратную замену. Вспоминаем, что .

Чистовое оформление рассмотренного примера должно выглядеть примерно так:

Значок не несет никакого математического смысла, он обозначает, что мы прервали решение для промежуточных объяснений.

Также всем рекомендую использовать математический знак вместо фразы «из этого следует это». И коротко, и удобно.

При оформлении примера в тетради надстрочную пометку обратной замены лучше выполнять простым карандашом.

Внимание! В следующих примерах нахождение дифференциала расписываться подробно не будет.

А теперь самое время вспомнить первый способ решения:

В чем разница? Принципиальной разницы нет. Это фактически одно и то же. Но с точки зрения оформления задания метод подведения функции под знак дифференциала – гораздо короче.

Возникает вопрос. Если первый способ короче, то зачем тогда использовать метод замены? Дело в том, что для ряда интегралов не так-то просто «подогнать» функцию под знак дифференциала.

Найти неопределенный интеграл.

Проведем замену: (другую замену здесь трудно придумать)

Как видите, в результате замены исходный интеграл значительно упростился – свёлся к обычной степенной функции. Это и есть цель замены – упростить интеграл.

Ленивые продвинутые люди запросто решат данный интеграл методом подведения функции под знак дифференциала:

Другое дело, что такое решение очевидно далеко не для всех студентов. Кроме того, уже в этом примере использование метода подведения функции под знак дифференциала значительно повышает риск запутаться в решении.

Найти неопределенный интеграл. Выполнить проверку.

Это пример для самостоятельного решения. Ответ в конце урока.

Найти неопределенный интеграл.

Замена:
Осталось выяснить, во что превратится

Хорошо, мы выразили, но что делать с оставшимся в числителе «иксом»?!
Время от времени в ходе решения интегралов встречается следующий трюк: мы выразим из той же замены !

Найти неопределенный интеграл.

Это пример для самостоятельного решения. Ответ в конце урока.

Найти неопределенный интеграл.

Наверняка некоторые обратили внимание, что в моей справочной таблице нет правила замены переменной. Сделано это сознательно. Правило внесло бы путаницу в объяснение и понимание, поскольку в вышерассмотренных примерах оно не фигурирует в явном виде.

Настало время рассказать об основной предпосылке использования метода замены переменной: в подынтегральном выражении должна находиться некоторая функция и её производная : (функции , могут быть и не в произведении)

В этой связи при нахождении интегралов довольно часто приходится заглядывать в таблицу производных.

В рассматриваемом примере замечаем, что степень числителя на единицу меньше степени знаменателя. В таблице производных находим формулу , которая как раз понижает степень на единицу. А, значит, если обозначить за знаменатель, то велики шансы, что числитель превратится во что-нибудь хорошее.

Кстати, здесь не так сложно подвести функцию под знак дифференциала:

Следует отметить, что для дробей вроде, такой фокус уже не пройдет (точнее говоря, применить нужно будет не только прием замены). Интегрировать некоторые дроби можно научиться на уроке Интегрирование некоторых дробей.

Вот еще пара типовых примеров для самостоятельного решения из той же оперы:

Найти неопределенный интеграл.

Найти неопределенный интеграл.

Решения в конце урока.

Найти неопределенный интеграл.

Смотрим в таблицу производных и находим наш арккосинус: . У нас в подынтегральном выражении находится арккосинус и нечто похожее на его производную.

Общее правило:
За обозначаем саму функцию (а не её производную).

В данном случае: . Осталось выяснить, во что превратится оставшаяся часть подынтегрального выражения .

В этом примере нахождение я распишу подробно поскольку – сложная функция.

Или короче:
По правилу пропорции выражаем нужный нам остаток:

Вот здесь подвести функцию под знак дифференциала уже не так-то просто.

Найти неопределенный интеграл.

Пример для самостоятельного решения. Ответ совсем близко.

Внимательные читатели заметили, что я рассмотрел мало примеров с тригонометрическими функциями. И это не случайно, поскольку под интегралы от тригонометрических функций отведён отдельный урок. Более того, на указанном уроке даны некоторые полезные ориентиры для замены переменной, что особенно актуально для чайников, которым не всегда и не сразу понятно, какую именно замену нужно проводить в том или ином интеграле. Также некоторые типы замен можно посмотреть в статье Определенный интеграл. Примеры решений.

Более опытные студенты могут ознакомиться с типовой заменой в интегралах с иррациональными функциями. Замена при интегрировании корней является специфической, и её техника выполнения отличается от той, которую мы рассмотрели на этом уроке.

Решения и ответы:

Пример 3: Решение:

Пример 4: Решение:

Пример 7: Решение:

Пример 9: Решение:

Пример 11: Решение:

Проведем замену:

Пример 12: Решение:

Проведем замену:

Пример 14: Решение:

Проведем замену:

Интегрирование подведением под знак дифференциала

Подведение под знак дифференциала — что это такое?

Подведение под знак дифференциала решает возникающую при интегрировании проблему, заключающуюся в том, что в подынтегральном выражении находится сложная функция, например, , , и т. п., а под знаком дифференциала d — просто икс. То есть нет возможности сразу применить таблицу интегралов для нахождения такого интеграла.

Цель подведения под знак дифференциала — получить простую функцию, которую можно интегрировать непосредственно, то есть по таблице интегралов. Тогда путём преобразований подынтегрального выражения получим простую функцию переменной и эта переменная будет находится и под знаком дифференциала d.

Решение заключается в том, что аргументом подынтегральной функции становится промежуточный аргумент («внутренняя» функция исходной сложной функции, например, , , и т. п.), который можно обозначить буквой u, и тот же промежуточный аргумент u подводится под знак дифференциала d.

После того, как такой интеграл будет найден, на место буквы u возвращается обозначаемый ею промежуточный аргумент, и таким образом будет окончательно найден интеграл исходной сложной функции.

Формальная общая запись описанных преобразований выглядит так:

где — «внешняя» функция, а — «внутренняя» функция или промежуточный аргумент.

В примерах вместо буквы u будем использовать букву t: так наши решения будут близки к наглядно понятному методу замены переменной. Кстати, в некоторых источниках метод подведения под знак дифференциала считается частным случаем метода замены переменной.

Повторим: наиболее частый случай, когда выгодно применять подведение под знак дифференциала — подынтегральное выражение представляет собой сложную функцию. Но это не единственный случай, когда требуется применять этот метод интегрирования. Другой распространённый случай — когда нет смысла использовать замену переменной, так как это делает вычисления громоздкими. Тогда, чтобы вычисления были короче, можно использовать подведение под знак дифференциала.

Пример 1. Найти подведением под знак дифференциала интеграл:

Решение. Внесём под знак дифференциала внутреннюю функцию. Это почти то же самое, что найти её производную. Получаем

Полученное нужно перенести в подынтегральное выражение, но в нём нет множителя-тройки перед дифференциалом. Значит, перед знаком интеграла ставим 1/3 и получаем:

Далее для получения простой функции обозначаем и и окончательно решаем как табличный интеграл 7:

Проверить решение задач на неопределённый интеграл можно на калькуляторе неопределённых интегралов онлайн.

Пример 2. Найти подведением под знак дифференциала интеграл:

Решение. Сразу же видим, что дифференциал синуса от икса равен косинусу от икса, а это как раз то, что нам нужно. Внесём под знак дифференциала синус от икса. Получаем

Полученное переносим в подынтегральное выражение:

Далее для получения простой функции обозначаем и и окончательно решаем как табличный интеграл 7:

Проверить решение задач на неопределённый интеграл можно на калькуляторе неопределённых интегралов онлайн.

Пример 3. Найти подведением под знак дифференциала интеграл:

Решение. Внесём под знак дифференциала внутреннюю функцию. Получаем

Полученное нужно перенести в подынтегральное выражение, но в нём нет множителя-двойки перед дифференциалом. Значит, перед знаком интеграла ставим 1/2 и получаем:

Далее для получения простой функции обозначаем и и окончательно решаем как табличный интеграл 7:

Применить подведение под знак дифференциала самостоятельно, а затем посмотреть решение

Следующие задачи — общий случай: решаются по определению дифференциала функции:

Пример 4. Найти подведением под знак дифференциала интеграл:

Пример 5. Найти подведением под знак дифференциала интеграл:

Продолжаем решать задачи вместе

В следующих задачах используются правила дифференцирования и интегрирования констант:

Так как , то , иными словами, константу можно подвести под знак дифференциала.

Пример 6. Найти подведением под знак дифференциала интеграл:

Так как , где C — произвольная константа, то .

Пример 7. Найти подведением под знак дифференциала интеграл:

Пример 8. Найти подведением под знак дифференциала интеграл:

Решение. Внесём под знак дифференциала внутреннюю функцию — минус икс в квадрате. Получаем

Полученное нужно перенести в подынтегральное выражение, но в нём нет множителя-минус двух перед дифференциалом. Значит, перед знаком интеграла ставим -1/2 и получаем:

Далее для получения простой функции обозначаем и и окончательно решаем как табличный интеграл 11:

Проверить решение задач на неопределённый интеграл можно на калькуляторе неопределённых интегралов онлайн.

Пример 9. Найти подведением под знак дифференциала интеграл:

Решение. Внесём под знак дифференциала внутреннюю функцию — логарифм икса. Получаем

Полученное нужно перенести в подынтегральное выражение:

Далее для получения простой функции обозначаем и и окончательно решаем как табличный интеграл 12:

Проверить решение задач на неопределённый интеграл можно на калькуляторе неопределённых интегралов онлайн.

Пример 10. Найти подведением под знак дифференциала интеграл:

Решение. Внесём под знак дифференциала внутреннюю функцию — ту, что в знаменателе. Получаем

Полученное нужно перенести в подынтегральное выражение, но в нём нет множителя-минус трёх перед дифференциалом. Значит, перед знаком интеграла ставим -1/3 и получаем:

Далее для получения простой функции обозначаем и и окончательно решаем как табличный интеграл 10:

Пример 11. Найти подведением под знак дифференциала интеграл:

Решение. Замечаем, что замена переменной в знаменателе выгодно оборачивается получением табличного интеграла 21 (с арктангенсом). Но в знаменателе у нас икс не в квадрате, а в шестой степени. Представляем икс в шестой степени как , а интеграл преобразуется к . Именно икс в кубе из второго слагаемого в знаменателе представляет собой внутреннюю функцию, которую внесём под знак дифференциала. Получаем

Полученное нужно перенести в подынтегральное выражение. В нём нет множителя-тройки перед дифференциалом. Значит, перед знаком интеграла ставим 1/3 и получаем:

Далее для получения простой функции обозначаем и и окончательно решаем как табличный интеграл 21:

Проверить решение задач на неопределённый интеграл можно на калькуляторе неопределённых интегралов онлайн.

Пример 12. Найти подведением под знак дифференциала интеграл:

Решение. Смотрим в числитель. Там косинус от трёх икс. Смотрим в знаменатель. Там присутствует синус также от трёх икс. Значит, всё выражение в знаменателе можем как внутреннюю функцию внести под знак дифференциала. Получаем

Полученное нужно перенести в подынтегральное выражение. В нём нет множителя-минус девяти перед дифференциалом. Значит, перед знаком интеграла ставим -1/9 и получаем:

Далее для получения простой функции обозначаем и и окончательно решаем как табличный интеграл 10:

Проверить решение задач на неопределённый интеграл можно на калькуляторе неопределённых интегралов онлайн.

Внесение под дифференциал

Назад Оглавление Вперед
1. Вынесение функции из-под знака дифференциала.

2. Внесение функции под знак дифференциала.
, где , т.е. является первообразной .
Пример:

[ Найдем первообразную функции ]

Итог:
3. Множитель-константу можно выносить за знак дифференциала и вносить под него (частный случай первого и второго правил).

Пример:
.
4. Под знаком дифференциала можно прибавлять или отнимать любую константу (частный случай второго правила).

Пример:

Следующие два правила не относятся к математическим формулам, однако их несоблюдение является одной из самых частых ошибок начинающих.

Одинаковое должно быть одинаковым.

Если в табличной формуле некоторые её части обозначены одинаковыми символами, то и в выражении, к которому будет применена эта формула, соответствующие части должны быть одинаковые.

Пример:

Для нахождения этого интеграла необходимо применить второй табличный интеграл , однако, в его записи знаменатель и переменная интегрирования одинаковы, а в исследуемом интеграле нет. Воспользуемся четвертым правилом, описанным выше: прибавим единицу под знаком дифференциала.

Здесь, для большей наглядности, можно сделать замену
.

Правило равновесия.

Если возникает необходимость домножить какую-либо часть выражения на константу, то тут же необходимо выполнить обратное действие, т.е. деление, на ту же константу.

Пример:

Здесь необходимо воспользоваться третьим табличным интегралом
,
но, по предыдущему правилу, в знаменателе первое слагаемое должно быть равно переменной дифференцирования, возведенной в квадрат. Проведем соответствующие преобразования: домножим под знаком дифференциала на 3 и поделим интеграл на 3. Т.к. уже сказано, что множитель-константу можно выносить как за знак дифференциала, так и за знак интеграла, а также можно вносить его обратно, то не принципиально где выполнить обратное действие. В данном случае удобнее уравновешивающий коэффициент поставить перед интегралом.

Сделаем замену . Воспользуемся табличной формулой, а потом и обратную замену.
. Это и есть ответ.

Примеры применения основных правил интегрирования.

Пример 1. Вычислить интеграл:

[ Для того, чтобы применить табличный интеграл №2, то есть получить натуральный логарифм, необходимо, чтобы переменная интегрирования и знаменатель были одинаковыми. Воспользуемся третьим правилом: ]

[ Воспользуемся четвертым правилом и прибавим под знаком дифференциала 3 : ]
[ Сделаем замену ] [ Воспользуемся табличным интегралом №2] [Сделаем обратную замену]
Ответ: .
Пример 2. Вычислить интеграл:

[ На первый взгляд непонятно к какому табличному интегралу стремиться, потому что ни в одной из формул нет ситуации, что в числителе стоит первая степень, а в знаменателе вторая. Применим второе правило: внесем под знак дифференциала. Найдем для этого первообразную для : . То есть: ]

[ По третьему правилу домножим и поделим соответствующие части интеграла на 4]
[ по четвертому правилу]
[ сделаем замену и воспользуемся табличным интегралом №2]

Ответ:

Задачи для самостоятельного решения:
Задание 1. Вычислить неопределенный интеграл:

+ Показать/спрятать подсказку №1.

+ Показать/спрятать подсказку №2.

+ Показать/спрятать подсказку №3.

+ Показать/спрятать Решение и Ответ.

Задание 2. Вычислить неопределенный интеграл:

+ Показать/спрятать подсказку №1.

+ Показать/спрятать подсказку №2.

+ Показать/спрятать подсказку №3.

+ Показать/спрятать Решение и Ответ.

Задание 3. Вычислить неопределенный интеграл:

+ Показать/спрятать подсказку №1.

+ Показать/спрятать подсказку №2.

+ Показать/спрятать подсказку №3.

+ Показать/спрятать Решение и Ответ.

Замечание: Вне зависимости от уровня знаний правил и приемов интегрирования настоятельно рекомендуется заучить следующие равенства, чаще всего используемые в тестовых заданиях:

Все эти равенства легко доказываются, однако, их необходимо помнить наизусть

Интегрирование внесением под дифференциал, формулы и примеры решений

Смотрим на таблицу интегралов и находим похожую формулу:.

Суть метода

Итак, внесение под знак интеграла опирается на следующее правило интегрирования. Если в произведении функции, стоящей под знаком интеграла, и дифференциала можно увидеть произведение другой функции и дифференциала от нее, то применяем подведение под знак дифференциала, то есть если

int» />

При внесении под знак дифференциала необходимо иметь в виду простейшие преобразования дифференциала:

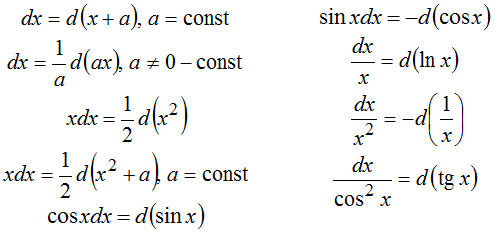
Очень часто метод внесения под знак дифференциала используют для нахождения интегралов вида

=frac<1>int=frac<1>Fleft( kx+b right)+C]» />

Поэтому имеют место следующие формулы для неопределенных интегралов:

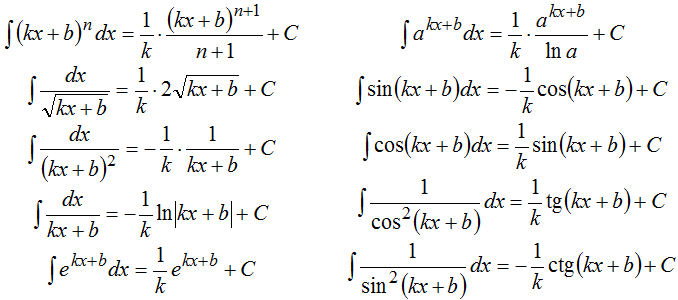
Первый способ

Так как $(3x+2)^2=9x^2+12x+4$, то $int (3x+2)^2 dx=int (9x^2+12x+4)dx$. Представляя интеграл $int (9x^2+12x+4)dx$ в виде суммы трёх интегралов и вынося константы за знаки соответствующих интегралов, получим:

$$int (9x^2+12x+4)dx=int 9x^2 dx+int 12x dx+int 4 dx=9cdot int x^2 dx+12cdot int x dx+4cdot int 1 dx$$

Чтобы найти $int x^2 dx$ подставим $u=x$ и $alpha=2$ в формулу №1 таблицы интегралов: $int x^2 dx=frac><2+1>+C=frac<3>+C$. Аналогично, подставляя $u=x$ и $alpha=1$ в ту же формулу из таблицы, будем иметь: $int x^1 dx=frac><1+1>+C=frac<2>+C$. Так как $int 1 dx=x+C$, то:

$$9cdot int x^2 dx+12cdot int x dx+4cdot int 1 dx=9cdotfrac<3>+12cdot frac<2>+4cdot x+C=3x^3+6x^2+4x+C.$$

Полное решение без пояснений таково:

$$int (9x^2+12x+4)dx=int 9x^2 dx+int 12x dx+int 4 dx=9cdot int x^2 dx+12cdot int x dx+4cdot int 1 dx==9cdotfrac<3>+12cdot frac<2>+4cdot x+C=3x^3+6x^2+4x+C.$$

11.1.4. Непосредственное интегрирование

Что такое непосредственное интегрирование? Это интегрирование с использованием свойств и простейшей таблицы интегралов (Интегралы). Рассмотренный метод подведения под знак дифференциала (занятие 11.1.

3) также относится к непосредственному интегрированию, так как нашей новой переменной служила линейная функция вида u=kx+b, но никаких новых букв мы не использовали, а просто применяли свойство VI (Интегралы), а именно:

Это свойство значительно расширяет таблицу простейших интегралов, так как в силу этого свойства таблица интегралов оказывается справедливой независимо от того, является переменная интегрирования независимой переменной или дифференцируемой функцией. В занятии 11.1.3. мы учились применять метод подведения переменной под знак дифференциала, используя формулы 1) и 2) (Интегралы), причем, прежде чем использовать тот или иной табличный интеграл, мы приводили данный интеграл к виду:

В примере 1 неявно подразумевалось u=9x-2, что и позволило нам применить свойство VI и формулу 5), в результате чего под знак дифференциала мы подвели (9х-2). Перед знаком интеграла стоит множитель 1/9, так как d (9x-2)=9dx.

1. Рассмотрим пример на применение формулы 4) (Интегралы), а именно, формулы:
3. 

В примере 2 неявно подразумевается u=25x-1, поэтому, под знак дифференциала подвели 25х-1, отсюда du=25dx. Вот почему перед интегралом стоит множитель 1/25.

Запись имеет метки: непосредственное интегрирование

Таблица первообразных

d(C)=0d(xn)=nxn-1dxd(ln(x))=dxxd(lognx)=dxx ln(n)d(ex)=exdxd(ax)=axln(a)dx

d(sin x)=cos xdxd(cos x)=-sin xdxd(tg x)=dx1+x2d(ctg) -dxsin2x

darcsin x=dx1-x2darccos x=-dx1-x2darctg x=dx1-x2darctg x=-dx1-x2

Подведение под знак дифференциала – что это такое?

Подведение под знак дифференциала решает возникающую при интегрировании проблему, заключающуюся в том, что в подынтегральном выражении находится сложная функция, например, , , и т. п., а под знаком дифференциала d – просто икс. То есть нет возможности сразу применить таблицу интегралов для нахождения такого интеграла.

Цель подведения под знак дифференциала – получить простую функцию, которую можно интегрировать непосредственно, то есть по таблице интегралов. Тогда путём преобразований подынтегрального выражения получим простую функцию переменной и эта переменная будет находится и под знаком дифференциала d.

Решение заключается в том, что аргументом подынтегральной функции становится промежуточный аргумент (“внутренняя” функция исходной сложной функции, например, , , и т. п.), который можно обозначить буквой u, и тот же промежуточный аргумент u подводится под знак дифференциала d.

После того, как такой интеграл будет найден, на место буквы u возвращается обозначаемый ею промежуточный аргумент, и таким образом будет окончательно найден интеграл исходной сложной функции.

Формальная общая запись описанных преобразований выглядит так:

где – “внешняя” функция, а – “внутренняя” функция или промежуточный аргумент.

В примерах вместо буквы u будем использовать букву t: так наши решения будут близки к наглядно понятному методу замены переменной. Кстати, в некоторых источниках метод подведения под знак дифференциала считается частным случаем метода замены переменной.

Повторим: наиболее частый случай, когда выгодно применять подведение под знак дифференциала – подынтегральное выражение представляет собой сложную функцию. Но это не единственный случай, когда требуется применять этот метод интегрирования. Другой распространённый случай – когда нет смысла использовать замену переменной, так как это делает вычисления громоздкими. Тогда, чтобы вычисления были короче, можно использовать подведение под знак дифференциала.

Пример 1. Найти подведением под знак дифференциала интеграл:

Решение. Внесём под знак дифференциала внутреннюю функцию. Это почти то же самое, что найти её производную. Получаем

Полученное нужно перенести в подынтегральное выражение, но в нём нет множителя-тройки перед дифференциалом. Значит, перед знаком интеграла ставим 1/3 и получаем:

Далее для получения простой функции обозначаем и и окончательно решаем как табличный интеграл 7:

Проверить решение задач на неопределённый интеграл можно на калькуляторе неопределённых интегралов онлайн.

Пример 2. Найти подведением под знак дифференциала интеграл:

Решение. Сразу же видим, что дифференциал синуса от икса равен косинусу от икса, а это как раз то, что нам нужно. Внесём под знак дифференциала синус от икса. Получаем

Полученное переносим в подынтегральное выражение:

Далее для получения простой функции обозначаем и и окончательно решаем как табличный интеграл 7:

Проверить решение задач на неопределённый интеграл можно на калькуляторе неопределённых интегралов онлайн.

Пример 3. Найти подведением под знак дифференциала интеграл:

Решение. Внесём под знак дифференциала внутреннюю функцию. Получаем

Полученное нужно перенести в подынтегральное выражение, но в нём нет множителя-двойки перед дифференциалом. Значит, перед знаком интеграла ставим 1/2 и получаем:

Далее для получения простой функции обозначаем и и окончательно решаем как табличный интеграл 7:

Одинаковое должно быть одинаковым.

Если в табличной формуле некоторые её части обозначены одинаковыми символами, то и в выражении, к которому будет применена эта формула, соответствующие части должны быть одинаковые.

Пример:

Для нахождения этого интеграла необходимо применить второй табличный интеграл , однако, в его записи знаменатель и переменная интегрирования одинаковы, а в исследуемом интеграле нет. Воспользуемся четвертым правилом, описанным выше: прибавим единицу под знаком дифференциала.

Здесь, для большей наглядности, можно сделать замену
.

Подведение числителя под знак дифференциала

Интегралы, которые мы будем рассматривать, похожи на интегралы предыдущего параграфа, они имеют вид: или

(коэффициенты a, b и f не равны нулю).

То есть, в числителе у нас появилась линейная функция. Как решать такие интегралы?

Пример 14

Найти неопределенный интеграл

• Пожалуйста, будьте внимательны, сейчас мы рассмотрим типовой алгоритм.
• 1) Когда дан интеграл вида
• или

(где коэффициенты a, b и f не равны нулю), то первое, что мы делаем, это… берём черновик. Дело в том, что сейчас нам предстоит выполнить небольшой подбор.

3) Раскрываем дифференциал:

Немного разные вещи получились…. А теперь нам нужно подобрать множитель для дифференциала , такой, чтобы при его раскрытии получилось, как минимум, 3x. В данном случае с подходящим множителем получится:

1. 4) Для самоконтроля снова раскрываем наш дифференциал:
2. Снова смотрим на числитель нашего интеграла:

. Уже ближе, но у нас получилось не «то» слагаемое (+2), а другое: (+3/2).

• 5) К нашему дифференциалу
• приписываем слагаемое, которое у нас изначально было в подынтегральной функции:
• .
• – Вычитаем (в данном случае – вычитаем, иногда нужно, наоборот, прибавлять)
• наше «не то» слагаемое:
• – Обе константы берем в скобки и приписываем справа значок дифференциала:
• – Вычитаем (в некоторых примерах нужно сложить) константы:
• .
• 6) Выполняем проверку:
• У нас получился в точности числитель подынтегральной функции, значит, подбор выполнен успешно.
• Чистовое оформление решения выглядит примерно так:

(1) Выполняем на черновике подбор числителя согласно вышерассмотренному алгоритму. Обязательно выполняем проверку, правильно ли выполнен подбор. При определенном опыте решения интегралов подбор нетрудно выполнить и в уме.

(2) Почленно делим числитель на знаменатель. В практическом решении задач данный шаг можно опускать

(3) Используя свойство линейности, разделяем интегралы. Все константы целесообразно вынести за знаки интегралов.

(4) Первый интеграл фактически является табличным, используем формулу (константу C припишем позже, когда возьмем второй интеграл). Во втором интеграле выделяем полный квадрат (такой тип интегралов мы рассмотрели в предыдущем параграфе). Остальное дело техники.

1. И, на закуску, пара примеров для самостоятельного решения – один проще, другой сложнее.
2. Пример 15
3. Найти неопределенный интеграл
4. .
5. Пример 16
6. Найти неопределенный интеграл
7. .
8. Для решения Примеров 15 и 16 будет полезен частный случай интегрирования степенной функции, которого нет в нашей справочной таблице:
9. .
10. Как видите, интегрирование дробей — дело кропотливое, часто приходится применять искусственные приемы и подборы. Но что делать…

Существуют и другие виды дробей, так называемые дробно-рациональные функции, они решаются методом неопределенных коэффициентов. Но это уже тема урока Интегрирование дробно рациональных функций.

• Решения и ответы:
• Пример 2: Решение:
• .
• Пример 4: Решение:
• .
• Пример 7: Решение:
• Пример 8: Решение:
• .
• Пример 10: Решение:
• .
• Пример 13: Решение:
• .
• Пример 15: Решение:
• Пример 16: Решение:
• .

Применить подведение под знак дифференциала самостоятельно, а затем посмотреть решение

Следующие задачи – общий случай: решаются по определению дифференциала функции:

Пример 4. Найти подведением под знак дифференциала интеграл:

Интегрирование подведением под знак дифференциала

Итак, внесение под знак интеграла опирается на следующее правило интегрирования. Если в произведении функции, стоящей под знаком интеграла, и дифференциала можно увидеть произведение другой функции и дифференциала от нее, то применяем подведение под знак дифференциала, то есть если

int» />

При внесении под знак дифференциала необходимо иметь в виду простейшие преобразования дифференциала:

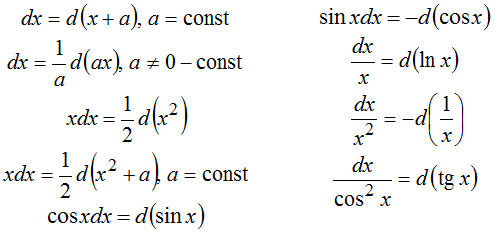
Очень часто метод внесения под знак дифференциала используют для нахождения интегралов вида

=frac<1>int=frac<1>Fleft( kx+b right)+C]» />

Поэтому имеют место следующие формулы для неопределенных интегралов:

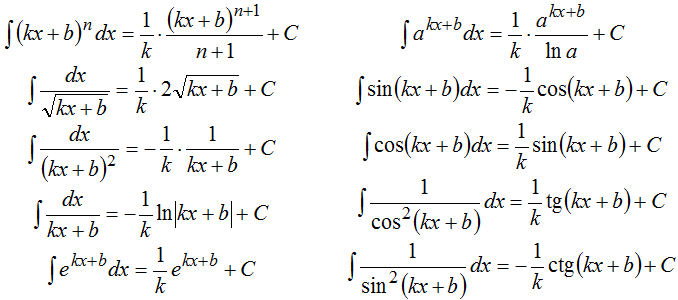
Первый способ

Так как $(3x+2)^2=9x^2+12x+4$, то $int (3x+2)^2 dx=int (9x^2+12x+4)dx$. Представляя интеграл $int (9x^2+12x+4)dx$ в виде суммы трёх интегралов и вынося константы за знаки соответствующих интегралов, получим:

$$int (9x^2+12x+4)dx=int 9x^2 dx+int 12x dx+int 4 dx=9cdot int x^2 dx+12cdot int x dx+4cdot int 1 dx$$

Чтобы найти $int x^2 dx$ подставим $u=x$ и $alpha=2$ в формулу №1 таблицы интегралов: $int x^2 dx=frac><2+1>+C=frac<3>+C$. Аналогично, подставляя $u=x$ и $alpha=1$ в ту же формулу из таблицы, будем иметь: $int x^1 dx=frac><1+1>+C=frac<2>+C$. Так как $int 1 dx=x+C$, то:

$$9cdot int x^2 dx+12cdot int x dx+4cdot int 1 dx=9cdotfrac<3>+12cdot frac<2>+4cdot x+C=3x^3+6x^2+4x+C.$$

Полное решение без пояснений таково:

$$int (9x^2+12x+4)dx=int 9x^2 dx+int 12x dx+int 4 dx=9cdot int x^2 dx+12cdot int x dx+4cdot int 1 dx==9cdotfrac<3>+12cdot frac<2>+4cdot x+C=3x^3+6x^2+4x+C.$$

Подведение функции под знак дифференциала

На уроке Неопределенный интеграл. Примеры решений мы научились раскрывать дифференциал, напоминаю пример, который я приводил:

То есть, раскрыть дифференциал – это формально почти то же самое, что найти производную.

Найти неопределенный интеграл. Выполнить проверку.

Смотрим на таблицу интегралов и находим похожую формулу: . Но проблема заключается в том, что у нас под синусом не просто буковка «икс», а сложное выражение. Что делать?

Подводим функцию под знак дифференциала:

Раскрывая дифференциал, легко проверить, что:

Фактически и – это запись одного и того же.

Но, тем не менее, остался вопрос, а как мы пришли к мысли, что на первом шаге нужно записать наш интеграл именно так: ? Почему так, а не иначе?

Формула (и все другие табличные формулы) справедливы и применимы НЕ ТОЛЬКО для переменной , но и для любого сложного выражения ЛИШЬ БЫ АРГУМЕНТ ФУНКЦИИ ( – в нашем примере) И ВЫРАЖЕНИЕ ПОД ЗНАКОМ ДИФФЕРЕНЦИАЛА БЫЛИ ОДИНАКОВЫМИ.

Поэтому мысленное рассуждение при решении должно складываться примерно так: «Мне надо решить интеграл . Я посмотрел в таблицу и нашел похожую формулу . Но у меня сложный аргумент и формулой я сразу воспользоваться не могу. Однако если мне удастся получить и под знаком дифференциала, то всё будет нормально. Если я запишу , тогда . Но в исходном интеграле множителя-тройки нет, поэтому, чтобы подынтегральная функция не изменилась, мне надо ее домножить на ». В ходе примерно таких мысленных рассуждений и рождается запись:

Теперь можно пользоваться табличной формулой :

Единственное отличие, у нас не буква «икс», а сложное выражение .

Выполним проверку. Открываем таблицу производных и дифференцируем ответ:

Получена исходная подынтегральная функция, значит, интеграл найден правильно.

Обратите внимание, что в ходе проверки мы использовали правило дифференцирования сложной функции . По сути дела подведение функции под знак дифференциала и – это два взаимно обратных правила.

Найти неопределенный интеграл. Выполнить проверку.

Анализируем подынтегральную функцию. Здесь у нас дробь, причем в знаменателе линейная функция (с «иксом» в первой степени). Смотрим в таблицу интегралов и находим наиболее похожую вещь: .

Подводим функцию под знак дифференциала:

Те, кому трудно сразу сообразить, на какую дробь нужно домножать, могут быстренько на черновике раскрыть дифференциал: . Ага, получается , значит, чтобы ничего не изменилось, мне надо домножить интеграл на .
Далее используем табличную формулу :

Получена исходная подынтегральная функция, значит, интеграл найден правильно.

Найти неопределенный интеграл. Выполнить проверку.

Это пример для самостоятельного решения. Ответ в конце урока.

Найти неопределенный интеграл. Выполнить проверку.

Это пример для самостоятельного решения. Ответ в конце урока.

При определенном опыте решения интегралов, подобные примеры будут казаться лёгкими, и щелкаться как орехи:

В конце данного параграфа хотелось бы еще остановиться на «халявном» случае, когда в линейной функции переменная входит с единичным коэффициентом, например:

Строго говоря, решение должно выглядеть так:

Как видите, подведение функции под знак дифференциала прошло «безболезненно», без всяких домножений. Поэтому на практике таким длинным решением часто пренебрегают и сразу записывают, что . Но будьте готовы при необходимости объяснить преподавателю, как Вы решали! Поскольку интеграла в таблице вообще-то нет.

Таблица первообразных

d(C)=0d(xn)=nxn-1dxd(ln(x))=dxxd(lognx)=dxx ln(n)d(ex)=exdxd(ax)=axln(a)dx

d(sin x)=cos xdxd(cos x)=-sin xdxd(tg x)=dx1+x2d(ctg) -dxsin2x

darcsin x=dx1-x2darccos x=-dx1-x2darctg x=dx1-x2darctg x=-dx1-x2

Одинаковое должно быть одинаковым.

Если в табличной формуле некоторые её части обозначены одинаковыми символами, то и в выражении, к которому будет применена эта формула, соответствующие части должны быть одинаковые.

Пример:

Для нахождения этого интеграла необходимо применить второй табличный интеграл , однако, в его записи знаменатель и переменная интегрирования одинаковы, а в исследуемом интеграле нет. Воспользуемся четвертым правилом, описанным выше: прибавим единицу под знаком дифференциала.

Здесь, для большей наглядности, можно сделать замену
.

Юникод

Кодировка по Юникоду, HTML и LaTeX

Знак	Юникод	Название	HTML-представление	LaTeX
Позиция	Название	Шестнадцатеричное	Десятичное	Мнемоника
∫	U+222B	integral	Интеграл	∫	∫	∫	int
∬	U+222C	double integral	Двойной интеграл	∬	∬	iint
∭	U+222D	triple integral	Тройной интеграл	∭	∭	iiint
∮	U+222E	contour integral	Интеграл по контуру	∮	∮	oint
∯	U+222F	surface integral	Интеграл по поверхности	∯	∯	oiint (требуется пакет esint)
∰	U+2230	volume integral	Интеграл по объёму	∰	∰	oiiint (требуется пакет esint)
∱	U+2231	clockwise integral	Интеграл с правым обходом	∱	∱
∲	U+2232	clockwise contour integral	Интеграл по контуру с правым обходом	∲	∲	ointclockwise (требуется пакет esint)
∳	U+2233	anticlockwise contour integral	Интеграл по контуру с левым обходом	∳	∳	ointctrclockwise (требуется пакет esint)
⨋	U+2A0B	summation with integral	⨋	⨋
⨌	U+2A0C	quadruple integral operator	Четырёхкратный интеграл	⨌	&#;
⨍	U+2A0D	finite part integral	⨍	⨌
⨎	U+2A0E	integral with double stroke	⨎	⨍
⨏	U+2A0F	integral average with slash	⨏	⨎
⨐	U+2A10	circulation function	⨐	⨏
⨑	U+2A11	anticlockwise integration	Интеграл с левым обходом	⨑	⨐
⨒	U+2A12	line integration with rectangular path around pole	⨒	⨑
⨓	U+2A13	line integration with semicircular path around pole	⨓	⨒
⨔	U+2A14	line integration not including the pole	⨔	⨓
⨕	U+2A15	integral around a point operator	⨕	⨔
⨖	U+2A16	quaternion integral operator	⨖	⨕
⨗	U+2A17	integral with leftwards arrow with hook	⨗	⨖
⨘	U+2A18	integral with times sign	⨘	⨗
⨙	U+2A19	integral with intersection	⨙	⨘
⨚	U+2A1A	integral with union	⨚	⨙
⨛	U+2A1B	integral with overbar	Верхний интеграл Дарбу	⨛	⨚
⨜	U+2A1C	integral with underbar	Нижний интеграл Дарбу	⨜	⨛

Традиции начертания

Русскоязычная традиция начертания знака интеграла отличается от принятой в некоторых западных странах.

В англоязычной традиции, реализованной в системе LaTeX, символ существенно наклонён вправо.