Какова частота колебаний поршней в цилиндрах двигателя автомобиля жигули

Глава V. Механические колебания и волны.

371. Шарик массой 200 г, закрепленный на пружине, жесткость которой 0,2 кН/м, совершает колеба­ния. Напишите уравнение, выражающее зависимость уско­рения от смещения: а_х(х). Каково наибольшее ускоре­ние, если амплитуда колебаний равна 1 см?

372. Найдите ускорение шарика при сме­щениях 2, 0 и -0,5 см, если масса шарика 100 г и жест­кость пружины 400 Н/м. В какой точке шарик движется с ускорением 10 м/с 2 ?

373. Маленький шарик, подвешенный на нити длиной 0,5 м, совершает колебания с амплитудой, много меньшей длины нити. Напишите формулу зависимости а_х (х), счи­тая движение прямолинейным. Каково ускорение шарика при смещениях 0,5 и -1 см?

374. Математический маятник длиной 1 м совершает колебания с амплитудой 2 см. Найдите тангенциальные уско­рения маятника в крайних положениях и в положении равновесия.

375. Амплитуда незатухающих колебаний точки струны 1 мм, частота 1 кГц. Какой путь пойдёт точка за 0,2 с?

3 76.Какова частота колебаний поршней в цилиндрах двигателя автомобиля «Жигули» при скорости движения автомобиля 120 км/ч, если диаметр колес 60 см и частота враще­ния коленчатого вала в 4,3 раза больше часто­ты вращения колес?

377. Уравнение дви­жения имеет вид: 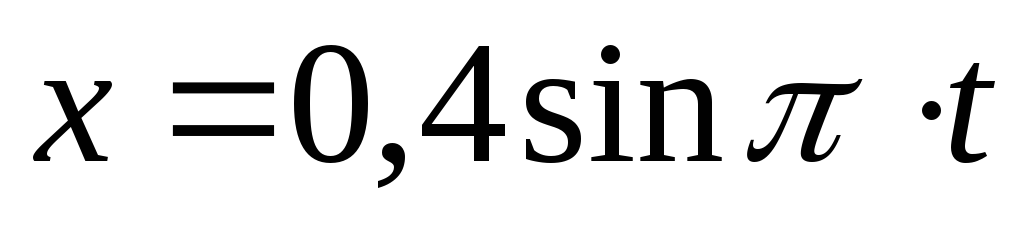. Како­вы амплитуда, частота, циклическая частота и период колебаний? Найдите смеще­ние через 0,25 с.

378. При каких фазах смещение по модулю равно по­ловине амплитуды?

379. По графику, приведенному на рисунке 105: а) найдите амплитуду, период, частоту и циклическую частоту колебаний; б) напишите уравнение зависимости 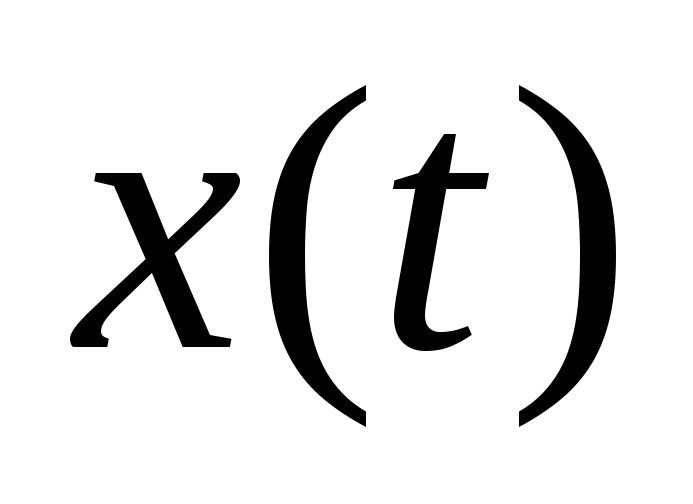, ,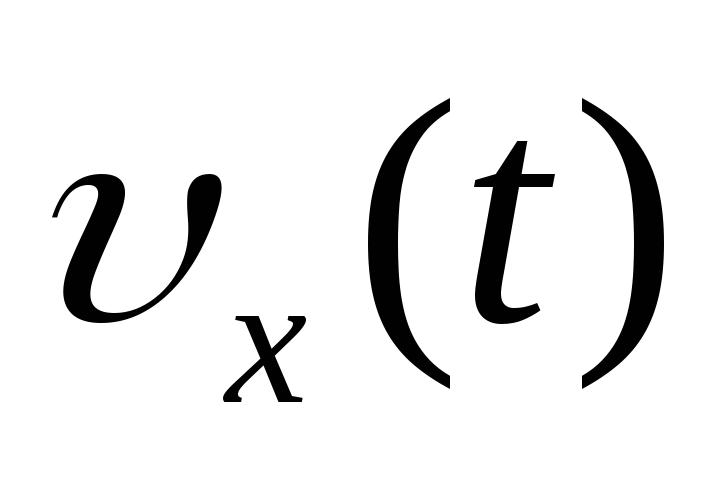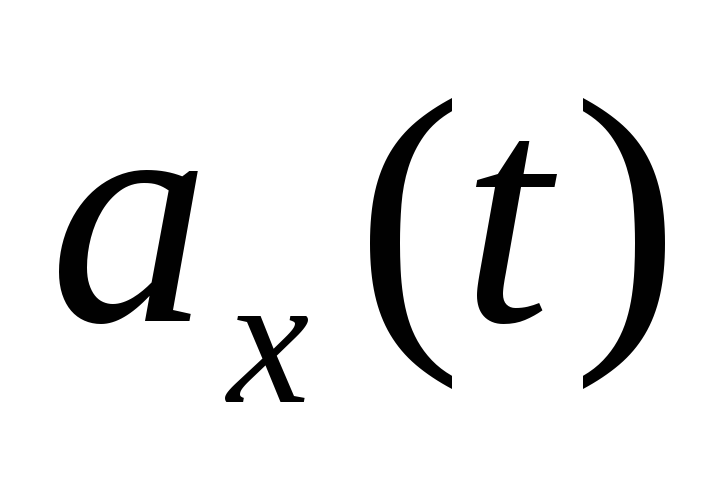; в) найдите ускорение колеблющейся точки при фазе 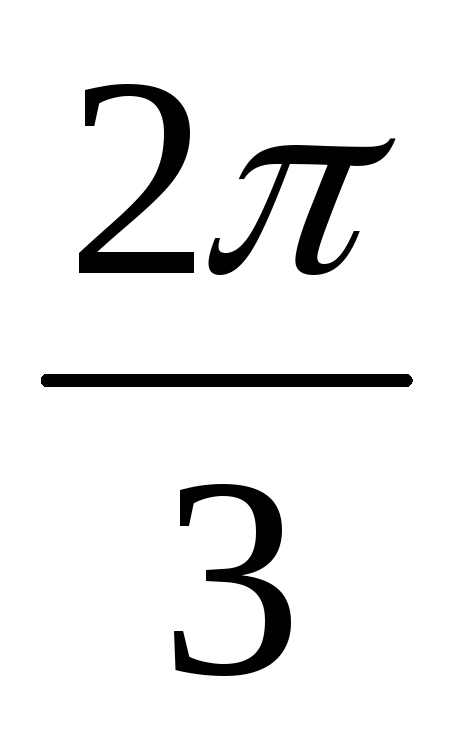; г) найдите скорость колеблющейся точки через 0,1 с после начала отсчета времени.

380. Амплитуда колебаний 10 см, а частота 0,5 Гц, На­пишите уравнение зависимости x(t). Найдите фазу и смещение через 1,5 с. Определите, через сколько времени смещение будет 7,1 см.

381. При фазе 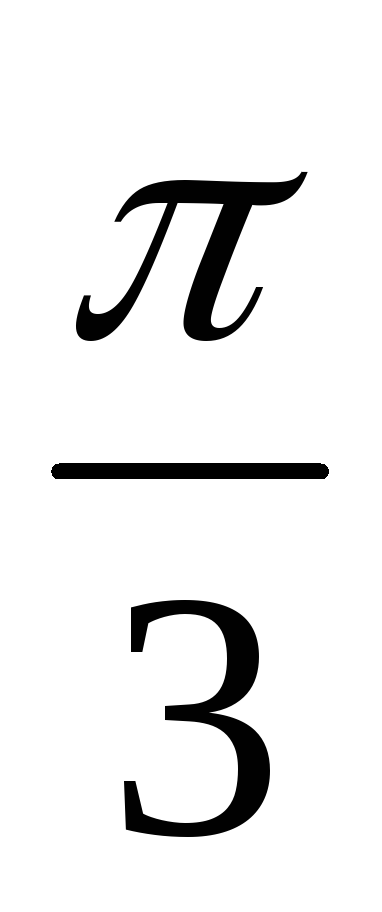рад смещение было равно 1 см. Найдите амплитуду колебаний и смещение при фазе.

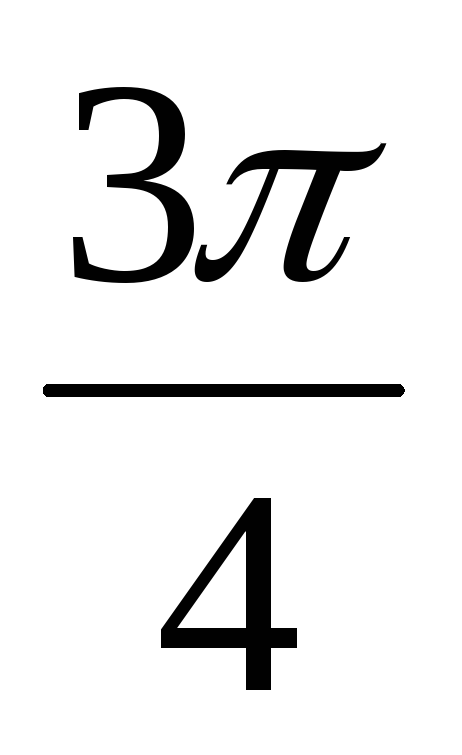382. Амплитуда колебаний конца ножки камертона 1 мм, а частота колебаний 500 Гц. Напишите уравнения 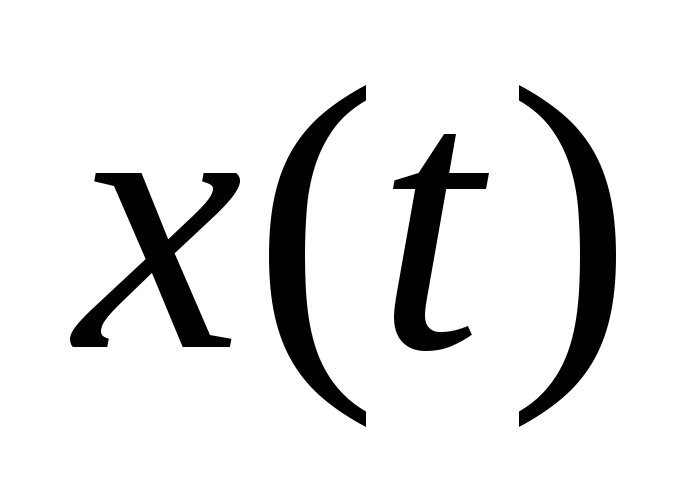, ,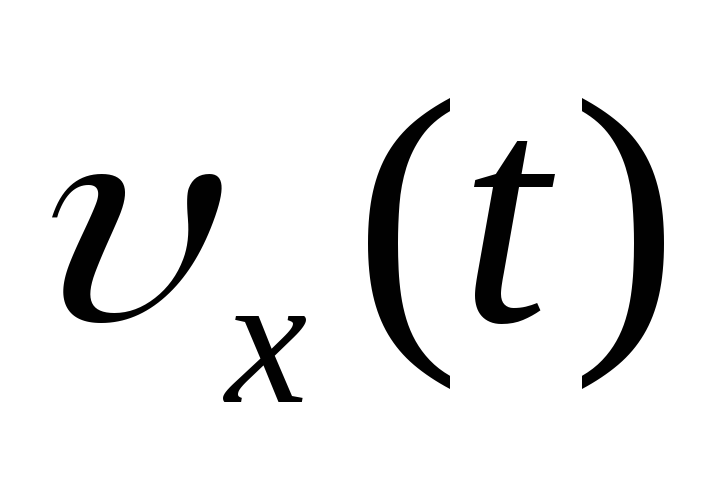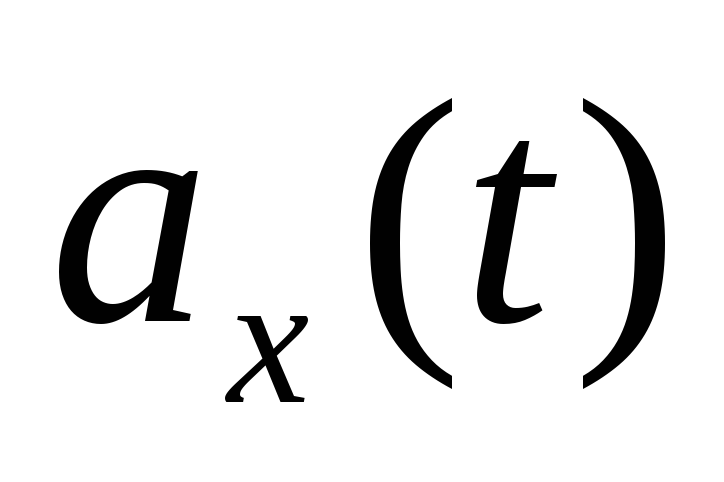.Каковы наибольшие значения скорос­ти и ускорения? В каких положениях достигаются эти значения?

1.2. Динамика и энергия колебаний

383. Найдите массу груза, который на пружине с жест­костью 250 Н/м делает 20 колебаний за 16 с.

384. Во сколько раз изменится частота колебаний ав­томобиля на рессорах после принятия груза, равного мас­се порожнего автомобиля?

385. Груз, подвешенный на пружине, совершает вертикальные колебания. Когда он имел массу m₁ период колебаний был равен 0,6 с, а когда его массу сделали равной m₂, период стал равен 0,8 с. Каким будет период колебаний этого груза, если его масса будет равна ?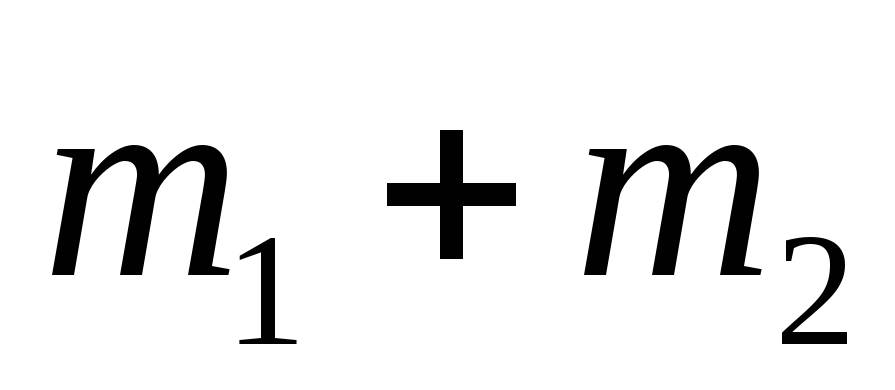

386. Медный шарик, подвешенный к пружине, совершает вертикальные колебания. Как изменится период колебаний, если к пружине подвесить алюминиевый шарик того же размера?

; .

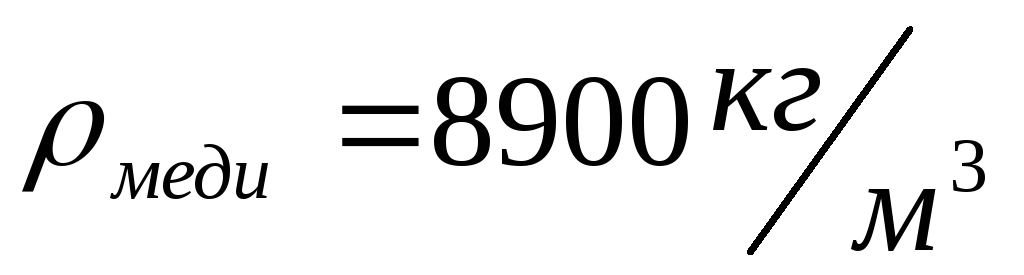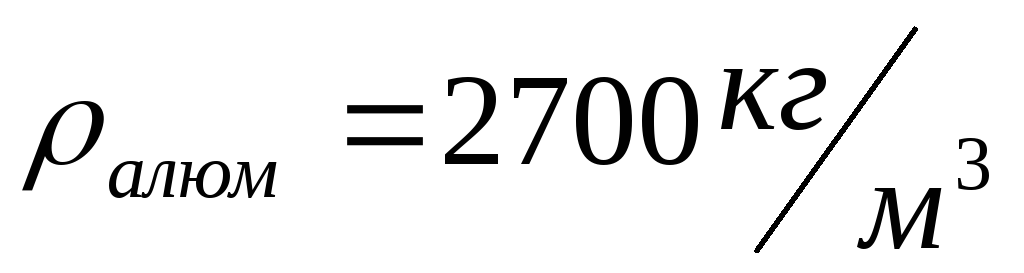387. Груз, подвешенный на длинном резиновом жгу­те, совершал вертикальные колебания с периодом Т. Во сколько раз из­менится период колебаний, если отрезать 3/4 длины жгу­та и подвесить на оставшуюся часть тот же груз?

388. Как относятся длины математических маятников, если за одно и то же время один из них совершает 10, а второй 30 колебаний?

389. За одно и то же время один математический ма­ятник делает 50 колебаний, а второй 30. Найдите их длины, если один из них на 32 см короче другого.

390. Один маятник имеет период колебаний 3 с, а другой 4 с. Каков период колебаний математического маятника, длина которого равна сумме длин указанных маятников?

391. Часы с маятником длиной 1 м за сутки отстают точно на 1 час. Что надо сделать с маятником, чтобы часы не отставали?

392. Шарик массой 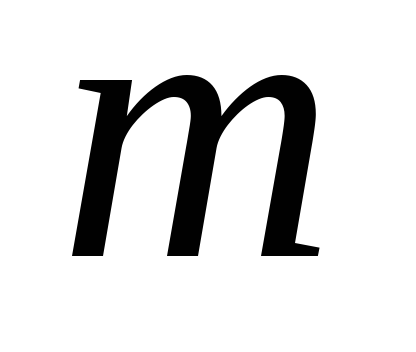, подвешенный на нити, совершает колебания (математический маятник). Как изменится частота колебаний, если шарику сообщить положительный заряди поместить его в однородное электрическое поле напряженностью, силовые линии которого направлены вертикально вниз?

393. В воде плавает брусок из дуба размерами 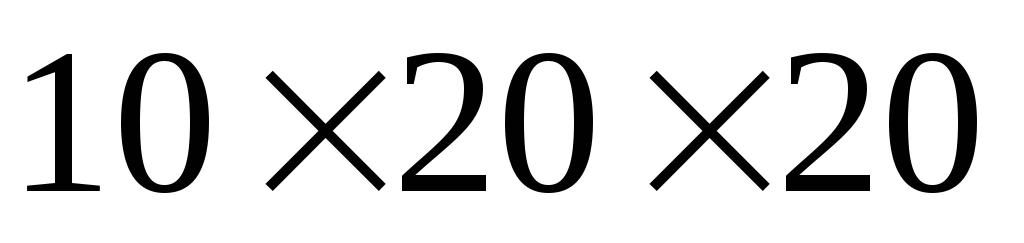см. Брусок слегка погрузили в воду и отпустили. Найдите период колебаний.

394. Математический маятник длиной 2,5 м совершает колебания с амплитудой 10 см. Напишите уравнение дви­жения x = x(t). Напи­шите формулу 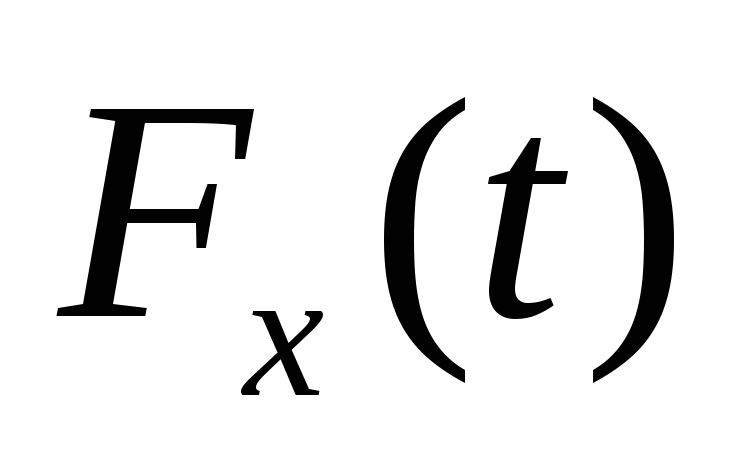, выражающую зависимость силы уп­ругости от времени. Найдите наибольшее значение силы уп­ругости и значение силы упругости через 1/12 периода. Масса маятника 1 кг.

395. Груз массой 400 г совершает колебания на пру­жине с жесткостью 250 Н/м. Амплитуда колебаний 15 см. Найдите полную механическую энергию колебаний и наи­большую скорость движения груза.

396. Груз, подвешенный на пружине с жесткостью 1 кН/м, колеблется с амплитудой 2 см. Найдите кинетическую и потенциальную энергию при фазе 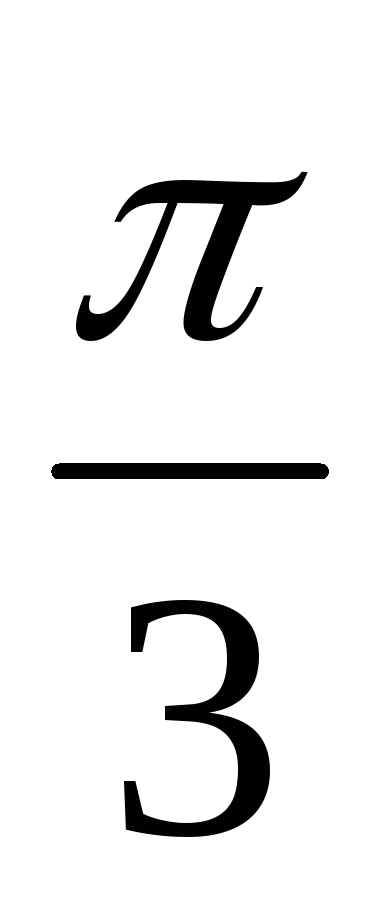рад.

397. Пружинный маятник вывели из положения равновесия и отпустили. Через какое время в долях периода кинетическая энергия колеблющегося тела будет равна потенциальной энергии пружины?

398. Пружинный маятник совершает гармонические колебания с амплитудой 4 см. При смещении груза на 3 см сила упругости рав­на 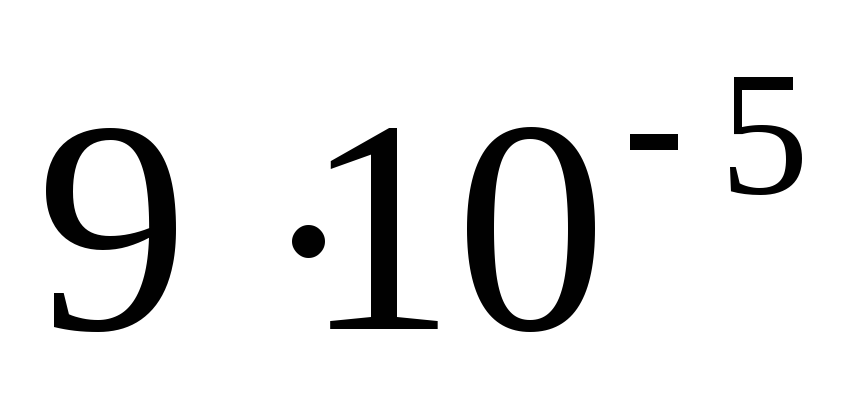Н. Определите потенциальную и кинетическую энергии,соответствующие данному смещению, и полную энергию маятника.

399. На нити подвешен груз массой 0,1 кг. Определите скорость и кинетическую энергию колеблющегося шарика при прохождении им положения равновесия, если повышение центра тяжести шарика при максимальном отклонении от положения равновесия 2,5 см.

400. Во сколько раз изменилась полная механическая энергия колеблющегося маятника при уменьшении его длины в 3 раза и увеличении амплитуды в 2 раза?

401. Маятник состоит из шарика массой 100 г, подвешенного на нити длиной 50 см. Определите период колебаний маятника и запас энергии, которым он обладает, если наибольший угол его отклонения от положения равновесия .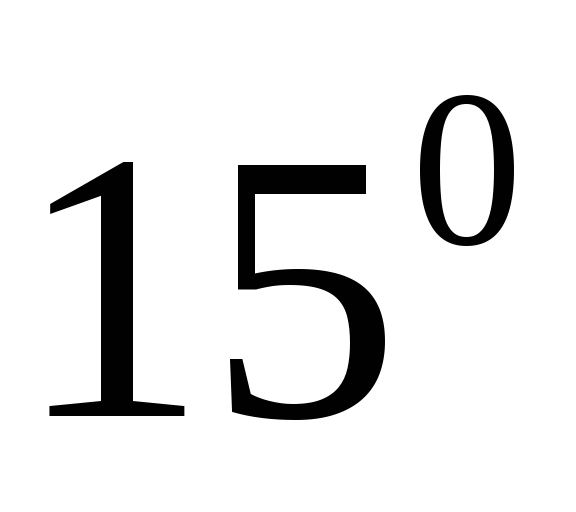

402. Мальчик несёт на коромысле ведра с водой, период собственных колебаний которых 1,6 с. При какой скорости движения вода особенно сильно начнет выплёскиваться, если длина шага мальчика 60 см?

Какова частота колебаний поршней в цилиндрах двигателя автомобиля жигули

371. Шарик массой 200 г, закрепленный на пружине, жесткость которой 0,2 кН/м, совершает колеба­ния. Напишите уравнение, выражающее зависимость уско­рения от смещения: ах(х). Каково наибольшее ускоре­ние, если амплитуда колебаний равна 1 см?

372. Найдите ускорение шарика при сме­щениях 2, 0 и -0,5 см, если масса шарика 100 г и жест­кость пружины 400 Н/м. В какой точке шарик движется с ускорением 10 м/с2?

373. Маленький шарик, подвешенный на нити длиной 0,5 м, совершает колебания с амплитудой, много меньшей длины нити. Напишите формулу зависимости ах (х), счи­тая движение прямолинейным. Каково ускорение шарика при смещениях 0,5 и -1 см?

374. Математический маятник длиной 1 м совершает колебания с амплитудой 2 см. Найдите тангенциальные уско­рения маятника в крайних положениях и в положении равновесия.

375. Амплитуда незатухающих колебаний точки струны 1 мм, частота 1 кГц. Какой путь пойдёт точка за 0,2 с?

376.Какова частота колебаний поршней в цилиндрах двигателя автомобиля «Жигули» при скорости движения автомобиля 120 км/ч, если диаметр колес 60 см и частота враще­ния коленчатого вала в 4,3 раза больше часто­ты вращения колес?

377. Уравнение дви­жения имеет вид: . Како­вы амплитуда, частота, циклическая частота и период колебаний? Найдите смеще­ние через 0,25 с.

378. При каких фазах смещение по модулю равно по­ловине амплитуды?

379. По графику, приведенному на рисунке 105: а) найдите амплитуду, период, частоту и циклическую частоту колебаний; б) напишите уравнение зависимости 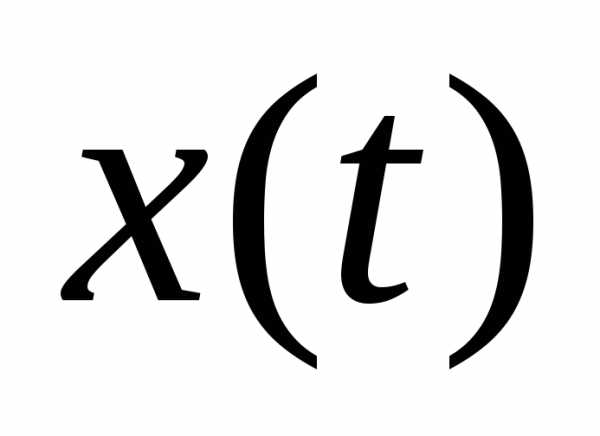, ,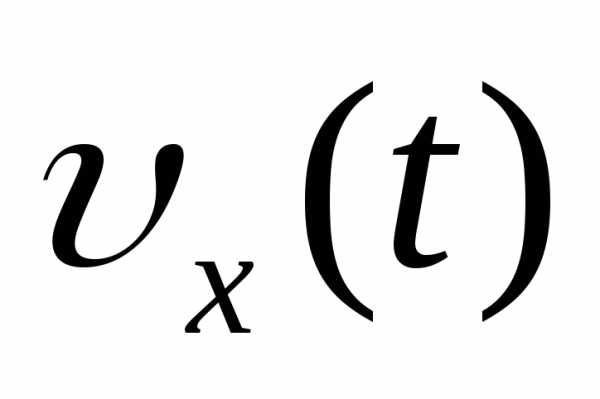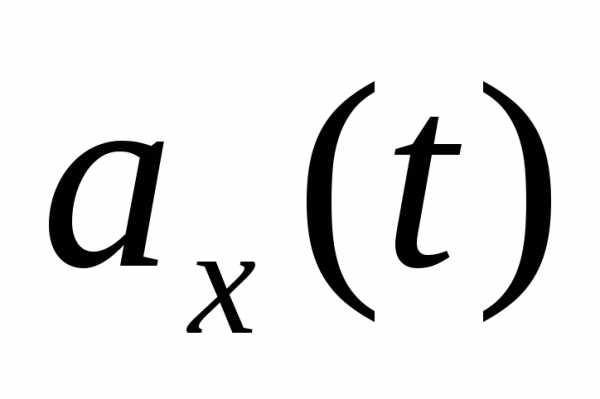; в) найдите ускорение колеблющейся точки при фазе 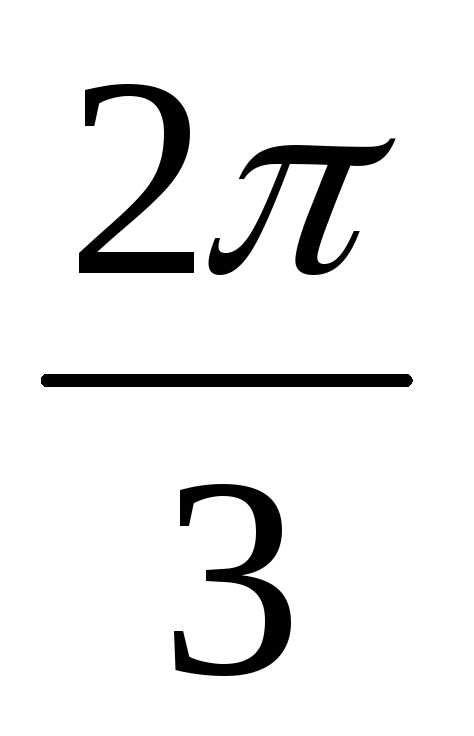; г) найдите скорость колеблющейся точки через 0,1 с после начала отсчета времени.

380. Амплитуда колебаний 10 см, а частота 0,5 Гц, На­пишите уравнение зависимости x(t). Найдите фазу и смещение через 1,5 с. Определите, через сколько времени смещение будет 7,1 см.

381. При фазе 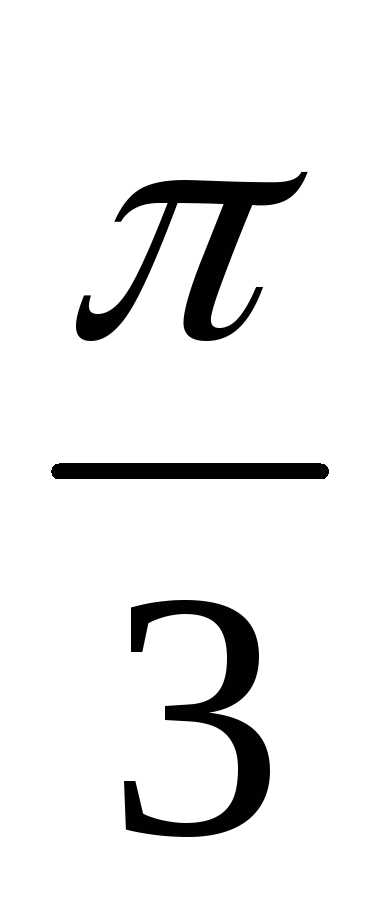рад смещение было равно 1 см. Найдите амплитуду колебаний и смещение при фазе.

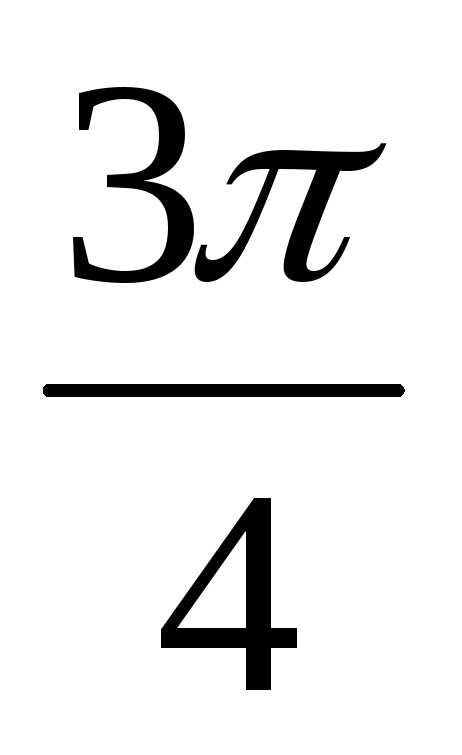382. Амплитуда колебаний конца ножки камертона 1 мм, а частота колебаний 500 Гц. Напишите уравнения 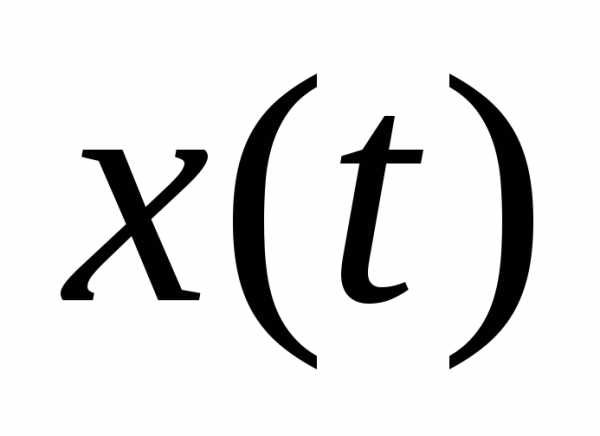, ,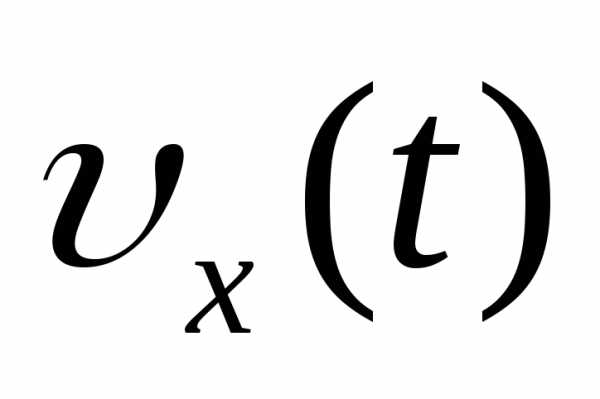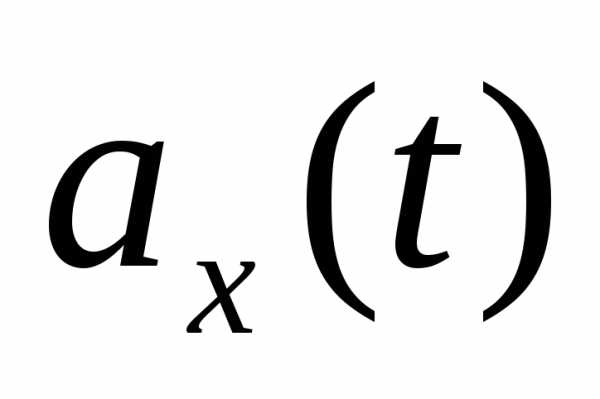.Каковы наибольшие значения скорос­ти и ускорения? В каких положениях достигаются эти значения?

1.2. Динамика и энергия колебаний

383. Найдите массу груза, который на пружине с жест­костью 250 Н/м делает 20 колебаний за 16 с.

384. Во сколько раз изменится частота колебаний ав­томобиля на рессорах после принятия груза, равного мас­се порожнего автомобиля?

385. Груз, подвешенный на пружине, совершает вертикальные колебания. Когда он имел массу m1 период колебаний был равен 0,6 с, а когда его массу сделали равной m2, период стал равен 0,8 с. Каким будет период колебаний этого груза, если его масса будет равна ?

386. Медный шарик, подвешенный к пружине, совершает вертикальные колебания. Как изменится период колебаний, если к пружине подвесить алюминиевый шарик того же размера?

387. Груз, подвешенный на длинном резиновом жгу­те, совершал вертикальные колебания с периодом Т. Во сколько раз из­менится период колебаний, если отрезать 3/4 длины жгу­та и подвесить на оставшуюся часть тот же груз?

388. Как относятся длины математических маятников, если за одно и то же время один из них совершает 10, а второй 30 колебаний?

389. За одно и то же время один математический ма­ятник делает 50 колебаний, а второй 30. Найдите их длины, если один из них на 32 см короче другого.

390. Один маятник имеет период колебаний 3 с, а другой 4 с. Каков период колебаний математического маятника, длина которого равна сумме длин указанных маятников?

391. Часы с маятником длиной 1 м за сутки отстают точно на 1 час. Что надо сделать с маятником, чтобы часы не отставали?

392. Шарик массой 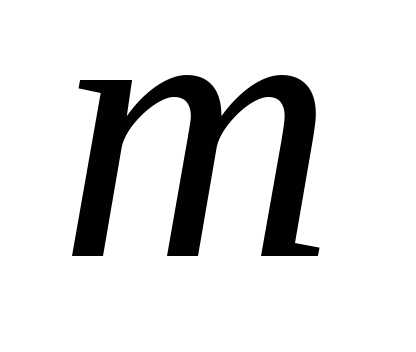, подвешенный на нити, совершает колебания (математический маятник). Как изменится частота колебаний, если шарику сообщить положительный заряди поместить его в однородное электрическое поле напряженностью, силовые линии которого направлены вертикально вниз?

393. В воде плавает брусок из дуба размерами см. Брусок слегка погрузили в воду и отпустили. Найдите период колебаний.

394. Математический маятник длиной 2,5 м совершает колебания с амплитудой 10 см. Напишите уравнение дви­жения x = x(t). Напи­шите формулу 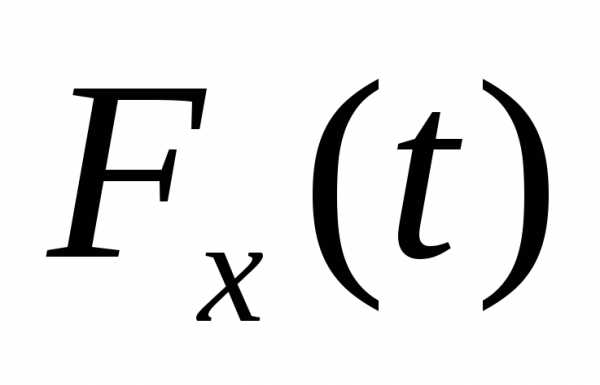, выражающую зависимость силы уп­ругости от времени. Найдите наибольшее значение силы уп­ругости и значение силы упругости через 1/12 периода. Масса маятника 1 кг.

395. Груз массой 400 г совершает колебания на пру­жине с жесткостью 250 Н/м. Амплитуда колебаний 15 см. Найдите полную механическую энергию колебаний и наи­большую скорость движения груза.

396. Груз, подвешенный на пружине с жесткостью 1 кН/м, колеблется с амплитудой 2 см. Найдите кинетическую и потенциальную энергию при фазе 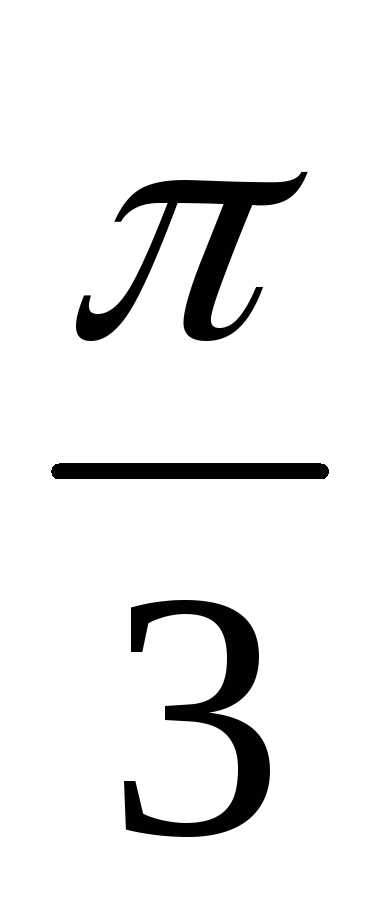рад.

397. Пружинный маятник вывели из положения равновесия и отпустили. Через какое время в долях периода кинетическая энергия колеблющегося тела будет равна потенциальной энергии пружины?

398. Пружинный маятник совершает гармонические колебания с амплитудой 4 см. При смещении груза на 3 см сила упругости рав­на 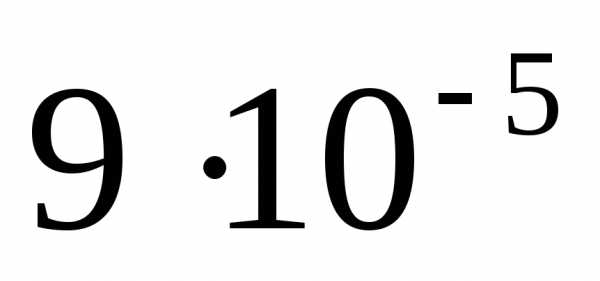Н. Определите потенциальную и кинетическую энергии,соответствующие данному смещению, и полную энергию маятника.

399. На нити подвешен груз массой 0,1 кг. Определите скорость и кинетическую энергию колеблющегося шарика при прохождении им положения равновесия, если повышение центра тяжести шарика при максимальном отклонении от положения равновесия 2,5 см.

400. Во сколько раз изменилась полная механическая энергия колеблющегося маятника при уменьшении его длины в 3 раза и увеличении амплитуды в 2 раза?

401. Маятник состоит из шарика массой 100 г, подвешенного на нити длиной 50 см. Определите период колебаний маятника и запас энергии, которым он обладает, если наибольший угол его отклонения от положения равновесия .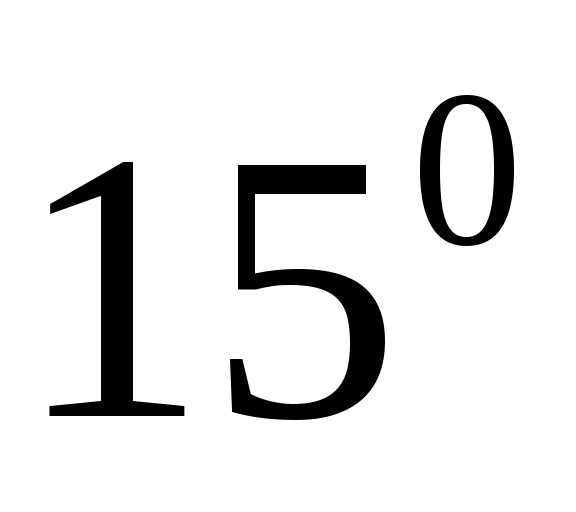

402. Мальчик несёт на коромысле ведра с водой, период собственных колебаний которых 1,6 с. При какой скорости движения вода особенно сильно начнет выплёскиваться, если длина шага мальчика 60 см?

Какова частота колебаний поршня двигателя автомобиля, если за 0,5 мин поршень совершает 600 колебаний?

Нашли ошибку? Сообщите в комментариях (внизу страницы)

Решение, ответ задачи 16944 из ГДЗ и решебников:

Для корректного отображения информации рекомендуем добавить наш сайт в исключения вашего блокировщика баннеров.

Идея нашего сайта — развиваться в направлении помощи ученикам школ и студентам. Мы размещаем задачи и решения к ним. Новые задачи, которые недавно добавляются на наш сайт, временно могут не содержать решения, но очень скоро решение появится, т.к. администраторы следят за этим. И если сегодня вы попали на наш сайт и не нашли решения, то завтра уже к этой задаче может появится решение, а также и ко многим другим задачам. основной поток посетителей к нам — это из поисковых систем при наборе запроса, содержащего условие задачи

858. Какова частота колебаний поршня двигателя автомобиля, если за 0,5 мин поршень совершает. решение задачи

Если к данной задачи нет решения — не переживайте. Наши администраторы стараются дополнять сайт решениями для тех задач и упражнения где это требуется и которые не даны в решебниках и сборниках с ГДЗ. Попробуйте зайти позже. Вероятно, вы найдете то, что искали 🙂

Задача 1. Поршень в цилиндре двигателя проходит

КОЛЕБАНИЯ И ВОЛНЫ.

Поршень в цилиндре двигателя проходит расстояние 66 мм между крайними положениями за . Принимая, что движение поршня происходит по гармоническому закону, определите максимальную скорость поршня.

Расстояние между крайними положениями поршня равно удвоенной амплитуде колебаний:

Отсюда амплитуда колебаний равна

Расстояние между крайними положениями поршень проходит за половину периода, поэтому период колебаний равен

Циклическая частота колебаний поршня равна

Амплитуда изменений скорости при гармонических колебаниях связана с амплитудой колебаний координаты и циклической частотой выражением

Влияние диаметра цилиндра и хода поршня на эффективный кпд двигателя внутреннего сгорания

Объём камеры сгорания в известной степени указывает на количество вводимой теплоты. Теплотворная способность поступающего заряда в бензиновом двигателе определена соотношением воздуха и топлива, близким к стехиометрическому. В дизель подаётся чистый воздух, а подача топлива ограничена степенью неполноты сгорания, при которой в отработавших газах появляется дым. Поэтому связь количества вводимой теплоты с объёмом камеры сгорания достаточно очевидна [2].

Наименьшим отношением поверхности к заданному объёму обладает сфера. Тепло в окружающее пространство отводится поверхностью, поэтому масса, имеющая форму шара, охлаждается в наименьшей степени. Эти очевидные соотношения учитываются при проектировании камеры сгорания. Следует, однако, иметь в виду геометрическое подобие деталей двигателей разных размеров. Как известно, объём сферы равен 4/3∙π∙R 3 , а её поверхность — 4∙π∙R 2 , и, таким образом, объём с ростом диаметра увеличивается быстрее, чем поверхность, и, следовательно, сфера большего диаметра будет иметь меньшую величину отношения поверхности к объёму. Если поверхности сферы разного диаметра имеют одинаковые перепады температур и одинаковые коэффициенты теплоотдачи α , то большая сфера будет охлаждаться медленнее.

Двигатели геометрически подобны, когда они имеют одинаковую конструкцию, но отличаются размерами. Если первый двигатель имеет диаметр цилиндра, например, равный единице, а у второго двигателя он в 2 раза больше, то все линейные размеры второго двигателя будут в 2 раза, поверхности — в 4 раза, а объёмы — в 8 раз больше, чем у первого двигателя. Полного геометрического подобия достичь, однако, не удаётся, так как размеры, например, свечей зажигания и топливных форсунок одинаковы у двигателей с разными размерами диаметра цилиндра.

Из геометрического подобия можно сделать тот вывод, что больший по размерам цилиндр имеет и более приемлемое отношение поверхности к объёму, поэтому его тепловые потери при охлаждении поверхности в одинаковых условиях будут меньше.

При определении мощности нужно, однако, учитывать некоторые ограничивающие факторы. Мощность двигателя зависит не только от размеров, т. е. объёма цилиндров двигателя, но и от частоты его вращения, а также среднего эффективного давления. Частота вращения двигателя ограничена максимальной средней скоростью поршня, массой и совершенством конструкции кривошипно-шатунного механизма. Максимальные средние скорости поршня бензиновых двигателей лежат в пределах 10—22 м/с. У двигателей легковых автомобилей максимальное значение средней скорости поршня достигает 15 м/с, а значения величины среднего эффективного давления при полной нагрузке близки к 1 МПа.

Рабочий объём двигателя и его размеры определяют не только геометрические факторы. Например, толщина стенок задана технологией, а не нагрузкой на них. Теплопередача через стенки зависит не от их толщины, а от теплопроводности их материала, коэффициентов теплоотдачи на поверхностях стенок, перепада температур и т. д. Колебания давления газа в трубопроводах распространяются со скоростью звука независимо от размеров двигателя, зазоры в подшипниках определяются свойствами масляной пленки и т. д. Некоторые выводы относительно влияния геометрических размеров цилиндров, тем не менее, необходимо сделать.

Преимущества и недостатки цилиндра с большим рабочим объёмом

Цилиндр большего рабочего объёма имеет меньшие относительные потери теплоты в стенки. Это хорошо подтверждается примерами стационарных дизелей с большими рабочими объёмами цилиндров, которые имеют очень низкие удельные расходы топлива. В отношении легковых автомобилей это положение, однако, подтверждается не всегда.

Анализ уравнения мощности двигателя показывает, что наибольшая мощность двигателя может быть достигнута при небольшой величине хода поршня.

Средняя скорость поршня может быть вычислена как

где S — ход поршня, м; n — частота вращения, мин -1 .

При ограничении средней скорости поршня Cп частота вращения может быть тем выше, чем меньше ход поршня. Уравнение мощности четырёхтактного двигателя имеет вид

где V_h — объём двигателя, дм 3 ; n — частота вращения, мин -1 ; p_e — среднее эффективное давление, МПа.

Следовательно, мощность двигателя прямо пропорциональна частоте его вращения и рабочему объёму. Тем самым к двигателю одновременно предъявляются противоположные требования — большой рабочий объём цилиндра и короткий ход. Компромиссное решение состоит в применении большего числа цилиндров.

Наиболее предпочтительный рабочий объём одного цилиндра высокооборотного бензинового двигателя составляет 300—500 см 3 . Двигатель с малым числом таких цилиндров плохо уравновешен, а с большим — имеет значительные механические потери и обладает поэтому повышенными удельными расходами топлива. Восьмицилиндровый двигатель рабочим объемом 3000 см 3 имеет меньший удельный расход топлива, чем двенадцатицилиндровый с таким же рабочим объёмом.

Для достижения малого расхода топлива целесообразно применять двигатели с малым числом цилиндров. Однако одноцилиндровый двигатель с большим рабочим объёмом не находит применения в автомобилях, поскольку его относительная масса велика, а уравновешивание возможно лишь при использовании специальных механизмов, что ведёт к дополнительному увеличению его массы, размеров и стоимости. Кроме того, большая неравномерность крутящего момента одноцилиндрового двигателя неприемлема для трансмиссий автомобиля.

Наименьшее число цилиндров у современного автомобильного двигателя равно двум. Такие двигатели с успехом применяют в автомобилях особо малого класса («Ситроен 2CV», «Фиат 126»). Сточки зрения уравновешенности, следующим в ряду целесообразного применения стоит четырёхцилиндровый двигатель, однако в настоящее время начинают применять и трёхцилиндровые двигатели с небольшим рабочим объёмом цилиндров, поскольку они позволяют получить малые расходы топлива. Кроме того, меньшее число цилиндров упрощает и удешевляет вспомогательное оборудование двигателя, так как сокращается число свечей зажигания, форсунок, плунжерных пар топливного насоса высокого давления. При поперечном расположении в автомобиле такой двигатель имеет меньшую длину и не ограничивает поворот управляемых колёс.

Трёхцилиндровый двигатель позволяет использовать унифицированные с четырёхцилиндровым основные детали: гильзу цилиндра, поршневой комплект, шатунный комплект, клапанный механизм. Такое же решение возможно и для пятицилиндрового двигателя, что позволяет при необходимости увеличения мощностного ряда вверх от базового четырёхцилиндрового двигателя избежать перехода на более длинный шестицилиндровый.

В дизелях помимо уменьшения потерь теплоты при сгорании большой рабочий объёмом цилиндра даёт возможность получить более компактную камеру сгорания, в которой при умеренных степенях сжатия создаются более высокие температуры к моменту впрыска топлива. У цилиндра с большим рабочим объёмом можно использовать форсунки с большим числом сопловых отверстий, обладающих меньшей чувствительностью к нагарообразованию.

Отношение хода поршня к диаметру цилиндра

Частное от деления величины хода поршня S на величину диаметра цилиндра D представляет собой широко употребляемое значение отношения S/D . Точка зрения на величину хода поршня в течение развития двигателестроения менялась.

На начальном этапе автомобильного двигателестроения действовала так называемая налоговая формула, на основе которой взимаемый налог на мощность двигателя рассчитывался с учетом числа и диаметра D его цилиндров. Классификация двигателей осуществлялась также в соответствии с этой формулой. Поэтому отдавалось предпочтение двигателям с большой величиной хода поршня с тем, чтобы увеличить мощность двигателя в рамках данной налоговой категории. Мощность двигателя росла, но увеличение частоты вращения было ограничено допустимой средней скоростью поршня. Поскольку механизм газораспределения двигателя в этот период не был рассчитан на высокую оборотность, то ограничение частоты вращения скоростью поршня не имело значения.

Как только описанная налоговая формула была упразднена, и классификация двигателей стада проводится в соответствии с рабочим объёмом цилиндра, ход поршня начал резко уменьшаться, что позволило увеличить частоту вращения и, тем самым, мощность двигателя. В цилиндрах большего диаметра стало возможным применение клапанов больших размеров. Поэтому были созданы короткоходные двигатели с отношением S/D , достигающим 0,5. Усовершенствование механизма газораспределения, особенно при использовании четырех клапанов в цилиндре, позволило довести номинальную частоту вращения двигателя до 10000 мин -1 и более, вследствие чего удельная мощность быстро возросла.

В настоящее время большое внимание уделяется уменьшению расхода топлива. Проведённые с этой целью исследования влияния S/D показали, что короткоходные двигатели обладают повышенным удельным расходом топлива. Это вызвано большой поверхностью камеры сгорания, а также снижением механического КПД двигателя из-за относительно большой величины поступательно движущихся масс деталей шатунно-поршневого комплекта и роста потерь на приводы вспомогательного оборудования. При очень коротком ходе нужно удлинять шатун с тем, чтобы нижняя часть юбки поршня не задевалась противовесами коленчатого вала. Масса поршня при уменьшении его хода мало уменьшилась и при использовании выемок и вырезов на юбке поршня. Для снижения выброса токсичных веществ в отработавших газах целесообразнее применять двигатели с компактной камерой сгорания и с более длинным ходом поршня. Поэтому в настоящее время от двигателей с очень низким отношением S/D отказываются.

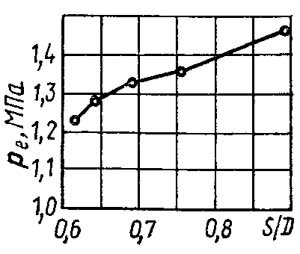Рис. 1
Влияние отношения хода поршня S к диаметру цилиндра D на среднее эффективное давление pe гоночных автомобилей

Зависимость среднего эффективного давления от отношения S/D у лучших гоночных двигателей, где четко видно снижение p_e при малых отношениях S/D , приведена на рис. 1. В настоящее время более выгодным считается отношение S/D , равное или несколько большее единицы. Хотя при коротком ходе поршня отношение поверхности цилиндра к его рабочему объёму при положении поршня в НМТ меньше, чем у длинноходных двигателей, нижняя зона цилиндра не так важна для отвода теплоты, поскольку температура газов уже заметно падает.

Длинноходный двигатель имеет более выгодное отношение охлаждаемой поверхности к объёму камеры сгорания при положении поршня в ВМТ, что более важно, так как в этот период цикла температура газов, определяющая потери теплоты, наиболее высока. Сокращение поверхности теплоотдачи в этой фазе процесса расширения уменьшает тепловые потери и улучшает индикаторный КПД двигателя.

Читайте также

Присадки для экономии топлива

Сегодня в ассортименте практически каждого автомобильного магазина среди разных товаров вы найдёте чудодейственные средства для автомобиля — так называемые присадки для экономии топлива.

«Облачные» вычисления преобразят салон автомобиля

«Облачные» вычисления могут изменить салон автомобиля. Хранение данных вне транспортного средства уменьшит беспорядок внутри.

Сноски

Мацкерле Ю. Современный экономичный автомобиль/Пер. с чешск. В. Б. Иванова; Под ред. А. Р. Бенедиктова. — М.: Машиностроение, 1987. — 320 с.: ил.//Стр. 186 — 192 (книга есть в библиотеке сайта). – Прим. icarbio.ru Узнать больше о эффективном КПД. – Прим. icarbio.ru

Комментарии

Добрый день. Я разработал 4х цилиндровый 4х тактник,но по принципу работы одноцилиндрового двс,т.е. все четыре цилиндра работают одновременно и от одной камеры сгорания,к тому же регулируемой.Комментарии или заинтересованность к моей разработке присылать на электронку. Разработка находится на стадии патентования. Спасибо.

34. Колебания — В.И. Лукашик, Сборник задач по физике

850. Свойством повторяемости обладают качания маятника часов, сезонные изменения температур, движение стрелки часов, колебания струны, вибрация крыльев самолета, движение Земли вокруг Солнца, колебания напряжения в сети электрического тока. Какие из перечисленных процессов можно назвать механическими колебательными процессами?
К механическим колебаниям относятся: качание маятника, движение стрелки часов, колебания струны, вибрация крыльев самолета, движение Земли вокруг Солнца.

851. Будут ли возможны колебания шарика, закрепленного на пружине, если вся система придет в состояние невесомости?
Да, поскольку колебания этой системы не зависят от силы тяжести.

852. Маятник часов совершает незатухающие гармонические колебания. Какие из величин — смещение, амплитуда, период, частота, скорость, ускорение — являются постоянными и какие переменными?
Постоянные: амплитуда, период, частота.
Переменные: смещение, скорость, ускорение.

853. Шарик, подвешенный на нити, совершает вращение в горизонтальной плоскости, описывая окружность диаметром d (рис. 244). Если наблюдение производится в плоскости вращения, то движение шарика воспринимается как гармоническое колебание. Чему равна амплитуда колебаний? Что можно сказать о частоте обращения шарика и частоте колебаний?
Амплитуда равна d/2; частота обращения равна частоте колебаний шарика.

854. Частота колебаний напряжения в электрической сети равна 50 Гц. Определите период колебания.

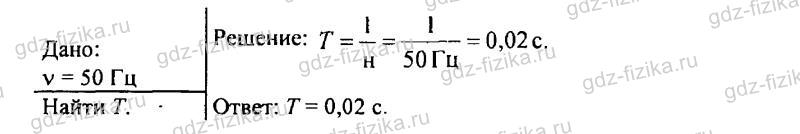
855. При измерении пульса человека было зафиксировано 75 пульсаций крови за 1 мин. Определите период сокращений сердечной мышцы.

856. У вала электрической швейной машинки частота вращения равна 1200 об/мин. За один оборот игла совершает одно колебание. Определите период колебания иглы.

857. Фреза имеет частоту вращения с 600 об/мин. Число зубьев на фрезе равно 40. С какой частотой вибрирует станок? Определите период вибраций.

858. Какова частота колебаний поршня двигателя автомобиля, если за 0,5 мин поршень совершает 600 колебаний?

859. Частота колебаний крыльев вороны в полете равна в среднем 3 Гц. Сколько взмахов крыльями сделает ворона, пролетев путь 650 м со скоростью 13 м/с?

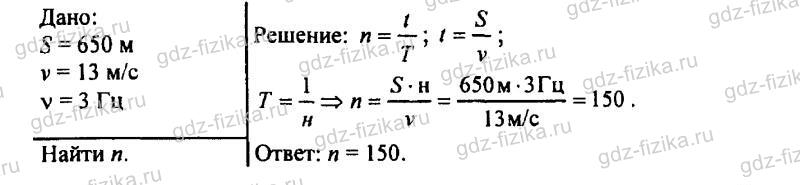
860. Для тела, совершающего свободные колебания, график зависимости смещения от времени представлен на рисунке 245. Определите период, частоту и амплитуду колебаний.

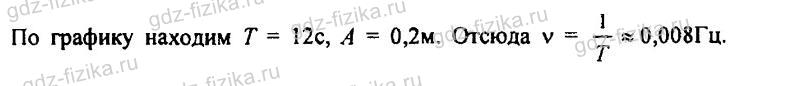
861. Колебания материальной точки описываются следующим уравнением: х =70 sin 0,5 t. Определите амплитуду колебаний и смещение точки от положения равновесия в следующие моменты времени: t1 = π/2 и t2 = π/3. При каких фазах смещение по модулю равно половине амплитуды?

862. Чему равна разность фаз свободных колебаний рук человека при ходьбе?
Разность фаз составляет π.

863. Гармоническое колебание описывается уравнением х = 2 sin (π/2t + π/4). Чему равны циклическая частота колебаний, линейная частота колебаний, начальная фаза колебаний?

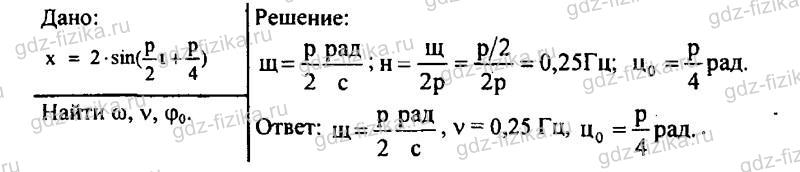
864. Можно ли предположить, что одно и то же колебание может быть описано с помощью следующих уравнений:
х = 3 sin (π/4 t+π/6), х = 3 cos(π/4 t + π/3), х = 3 cos (π/4 t – π/3)?
Да.

865. В какие моменты времени скорость колеблющейся материальной точки равна нулю, если колебание описывается уравнением х = 4 sin π/2 t ?

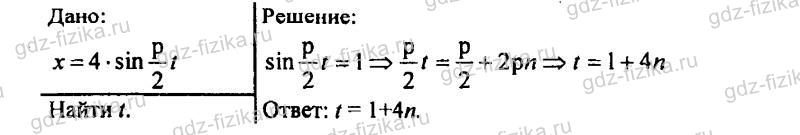
866. Максимально или минимально ускорение в те моменты времени, когда скорость колеблющегося пружинного маятника равна 0?
Максимально.

867. Что можно сказать об ускорении, которое испытывает колеблющийся груз, подвешенный на пружине, в момент прохождения положения равновесия?
Ускорение максимально.

868. В момент начала наблюдения нить маятника длиной l (рис. 246) образует с вертикалью малый угол α, а груз находится в крайнем положении. Можно ли считать угол α начальной фазой колебаний? Как вычислить амплитуду колебаний?
α нельзя считать начальной фазой. А =l sin α, где А — амплитуда колебаний.

869. Каково направление равнодействующей сил, приложенных к грузу маятника (рис. 246), когда этот груз находится в крайних положениях; проходит положение равновесия?
При нахождении груза в крайних положениях равнодействующая сил направлена по касательной к дуге, описываемой грузами. В положении равновесия она равна 0.

870. Почему на доску качелей встать в полный рост труднее всего в тот момент, когда качели проходят положение равновесия?
Потому что в этот момент доска имеет наибольшую скорость.

871. Чему равен период колебания математического маятника, если длина нити равна 9,8 м?

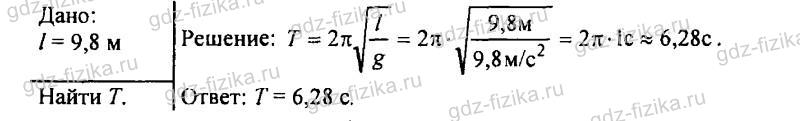
872. Два математических маятника совершают свободные колебания. Графики зависимости смещения от времени представлены на рисунке 247. Определите период колебания каждого из маятников и отношение длин маятников.

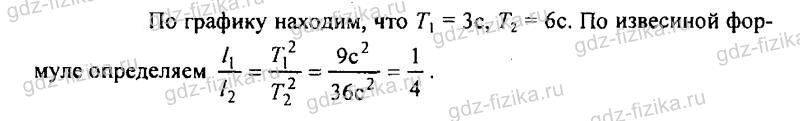
873. Математический маятник длиной 0,99 м совершает 50 полных колебаний за 1 мин 40 с. Чему равно ускорение свободного падения в данном месте на поверхности Земли?

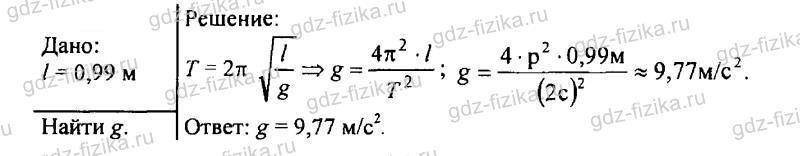
874. Во сколько раз надо изменить длину математического маятника, чтобы период колебания изменился в 2 раза?
Так как период пропорционален корню квадратному из длины, то для удвоения периода длину следует увеличить в 4 раза.

875. Из двух математических маятников в одном и том же месте Земли один совершает 40 колебаний за некоторое время, а другой за то же время — 20 колебаний. Определите длину каждого из маятников, если один из них длиннее другого на 90 см.

876. В покоящейся ракете колеблется математический маятник. При движении ракеты вверх с некоторым ускорением период колебания маятника уменьшился вдвое. Во сколько раз ускорение, с которым движется ракета, больше ускорения свободного падения?

877. Груз массой 50 г, прикрепленный к пружине, жесткость которой равна 0,49 Н/м, совершает колебания. Какой длины надо взять математический маятник, чтобы его частота колебаний была равна частоте колебаний пружинного маятника?

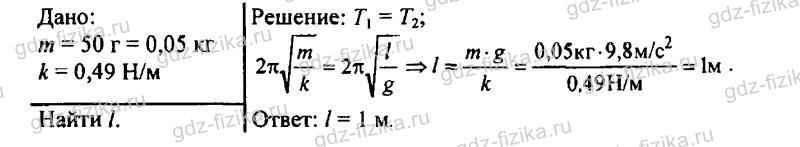
878. Как изменится период и частота колебаний упругой доски, установленной на вышке для прыжков в воду, если после взрослого человека на доске раскачивается мальчик, готовясь к прыжку?
Период уменьшится, частота увеличится.

879. Когда груз неподвижно висел на вертикальной пружине, ее удлинение было равно 5 см. Затем груз оттянули вниз и отпустили, вследствие чего он начал колебаться. Каков период колебания?

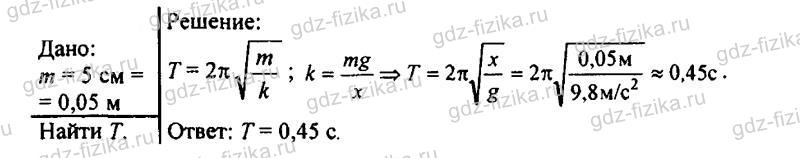
880. Шарик с отверстием, прикрепленный к легкой пружине жесткостью 250 Н/м, может совершать незатухающие колебания вдоль стержня (рис. 248). Чему равно ускорение, испытываемое шариком (Рис. 248) в положении равновесия и в крайних положениях, если амплитуда колебаний равна 4 см, а масса 50 г?

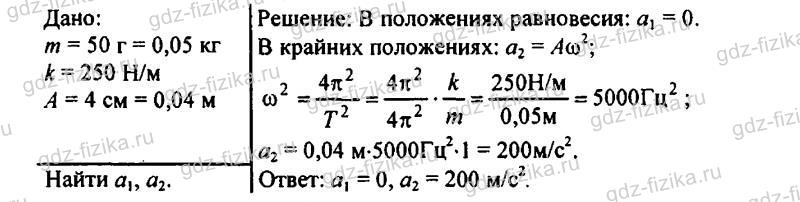
881. Опишите превращения механической энергии, совершающиеся в процессе свободных незатухающих колебаний пружинного маятника в горизонтальном направлении; в вертикальном направлении. Сохраняется ли полная механическая энергия в процессе колебаний?
В горизонтальном направлении: в положении равновесия: Еп пр = 0; Екин – мах. В крайних положениях: Екин = 0; Еп пр – мах. В вертикальном направлении: положение равновесия сместится вниз от точки подвеса маятника за счет потенциальной энергии груза, скомпенсированной потенциальной энергией пружины. Превращения энергии осуществляются точно также, как и в горизонтальном направлении. Полная механическая энергия остается неизменной.

882. Груз массой 400 г совершает колебания на пружине жесткостью 250 Н/м. Амплитуда колебаний равна 15 см. Чему равны полная механическая энергия колебаний и наибольшая скорость движения груза?

883. По условию задачи 880 определите полную энергию колебаний шарика, а также потенциальную и кинетическую энергии в тот момент, когда шарик находится в точке с координатой х = 2 см. За начало отсчета примите положение равновесия шарика.

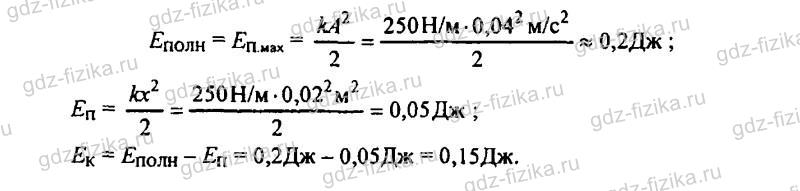
884. Груз, подвешенный на пружине жесткостью 1 кН/м, колеблется с амплитудой 2 см по закону: х = A sin (ώt + φ0). Определите кинетическую и потенциальную энергии при фазе π/6 рад.

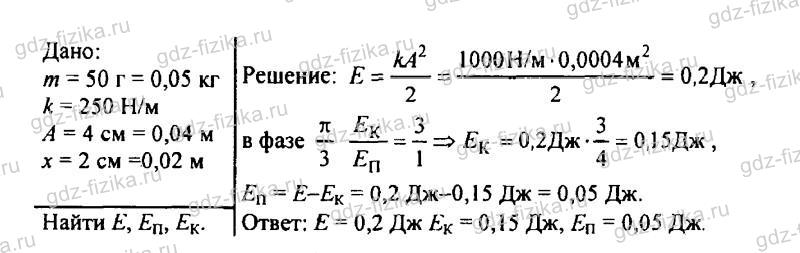
885. Почему легче идти в обуви на толстой упругой подошве при определенной частоте шагов? Объясните с точки зрения превращения энергии.
При определенной частоте шагов циклическая частота со вынуждающей силы приближается к циклической частоте со0 колебательной системы — упругой подошвы. Возникает резонанс.

886. Как изменяется амплитуда и какие превращения претерпевает энергия при колебаниях дерева при одиночном порыве ветра; автомобиля при работе двигателя на холостом ходу; коромысла весов при взвешивании?
При колебании дерева, при одиночном порыве ветра, и коромысла весов при взвешивании амплитуда и энергия уменьшаются с каждым последующим колебанием.

887. Вода, которую мальчик несет в ведре, начинает сильно расплескиваться. Мальчик меняет темп ходьбы или просто «сбивает ногу», и расплескивание прекращается. Почему так происходит?
Мальчик меняет фазу своих колебаний. Колебания воды гасятся за счет колебаний мальчика.

888. Максимальную амплитуду вертикальных колебаний мячика, подвешенного на тонкой резинке, можно получить, если его нести, делая за 1 мин 48 шагов. Определите коэффициент упругости резинки, если масса мячика равна 60 г.

Какова частота колебаний поршней в цилиндрах двигателя автомобиля жигули

КОЛЕБАНИЯ

Задание 850.

Свойством повторяемости обладают качания маятника часов, сезонные изменения температур, движение стрелки часов, колебания струны, вибрация крыльев самолета, движение Земли вокруг Солнца, колебания напряжения в сети электрического тока. Какие из перечисленных процессов можно назвать механическими колебательными процессами?

Задание 851.

Будут ли возможны колебания шарика, закрепленного на пружине, если вся система придет в состояние невесомости?

Задание 852.

Маятник часов совершает незатухающие гармонические колебания. Какие из величин — смещение, амплитуда, период, частота, скорость, ускорение — являются постоянными и какие переменными?

Задание 853.

Шарик, подвешенный на нити, совершает вращение в горизонтальной плоскости, описывая окружность диаметром d (рис. 244). Если наблюдение производится в плоскости вращения, то движение шарика воспринимается как гармоническое колебание. Чему равна амплитуда колебаний? Что можно сказать о частоте обращения шарика и частоте колебаний?

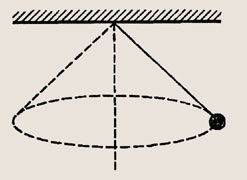
Рис.244

Задание 854.

Частота колебаний напряжения в электрической сети равна 50 Гц. Определите период колебания.

Задание 855.

При измерении пульса человека было зафиксировано 75 пульсаций крови за 1 мин. Определите период сокращений сердечной мышцы.

Задание 856.

У вала электрической швейной машинки частота вращения равна 1200 об/мин. За один оборот игла совершает одно колебание. Определите-период колебания иглы.

Задание 857.

Фреза станка имеет частоту вращения 600 об/мин. Число зубьев на фрезе равно 40. С какой частотой вибрирует станок? Определите период вибраций.

Задание 858.

Какова частота колебаний поршня двигателя автомобиля, если за 0,5 мин поршень совершает 600 колебаний?

Задание 859.

Частота колебаний крыльев вороны в полете равна в среднем 3 Гц. Сколько взмахов крыльями сделает ворона, пролетев путь 650 м со скоростью 13 м/с?

Задание 860.

Для тела, совершающего свободные колебания, график зависимости смещения от времени представлен на рисунке 245. Определите период, частоту и амплитуду колебаний.

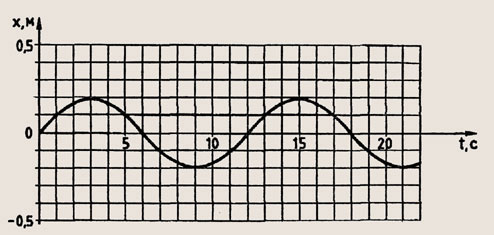
Рис.245

Задание 861.

Колебания материальной точки описываются следующим уравнением: х= 70 sin 0,5 t. Определите амплитуду колебаний и смещение точки от положения равновесия в следующие моменты времени:

При каких фазах смещение по модулю равно половине амплитуды?

Задание 862.

Чему равна разность фаз свободных колебаний рук человека при ходьбе?

Задание 863.

Гармоническое колебание описывается уравнением:

Чему равны циклическая частота колебаний, линейная частота, начальная фаза колебаний?

Задание 864.

Можно ли предположить, что одно и то же колебание может быть описано с помощью следующих уравнений:

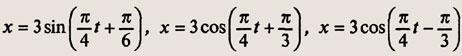
Задание 865.

В какие моменты времени скорость колеблющейся материальной точки равна нулю, если колебание описывается уравнением

Задание 866.

Максимально или минимально ускорение в те моменты времени, когда скорость колеблющегося пружинного маятника равна 0?

Задание 867.

Что можно сказать об ускорении, которое испытывает колеблющийся груз, подвешенный на пружине, в момент прохождения положения равновесия?

Задание 868.

В момент начала наблюдения нить маятника длиной L(рис. 246) образует с вертикалью малый угол a, a груз находится в крайнем положении. Можно ли считать угол α начальной фазой колебаний? Как вычислить амплитуду колебаний?

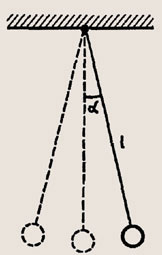
Рис.246

Задание 869.

Каково направление равнодействующей сил, приложенных к грузу маятника (рис. 246), когда этот груз находится в крайних положениях; проходит положение равновесия?

Задание 870.

Почему на доску качелей встать в полный рост труднее всего в тот момент, когда качели проходят положение равновесия?

Задание 871.

Чему равен период колебания математического маятника, если длина нити равна 9,8 м?

Задание 872.

Два математических маятника совершают свободные колебания. Графики зависимости смещения от времени представлены на рисунке 247. Определите период колебания каждого из маятников и отношение длин маятников.

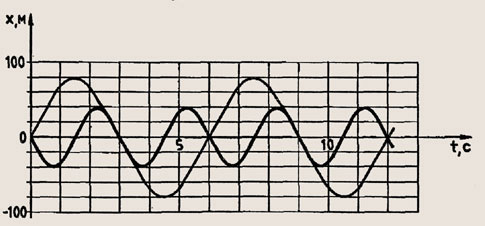
Рис. 247

Задание 873.

Математический маятник длиной 0,99 м совершает 50 полных колебаний за 1 мин 40 с. Чему равно ускорение свободного падения в данном месте на поверхности Земли? Можно принять

Задание 874.

Во сколько раз надо изменить длину математического маятника, чтобы период колебания изменился в 2 раза?

Задание 875.

Из двух математических маятников в одном и том же месте Земли один совершает 40 колебаний за некоторое время, а другой за то же время — 20 колебаний. Определите длину каждого из маятников, если один из них длиннее другого на 90 см.

Задание 876.

В покоящейся ракете колеблется математический маятник. При движении ракеты вверх с некоторым ускорением период колебания маятника уменьшился вдвое. Во сколько раз ускорение, с которым движется ракета, больше ускорения свободного падения?

Задание 877.

Груз массой 50 г, прикрепленный к пружине, жесткость которой равна 0,49 Н/м, совершает колебания. Какой длины надо взять математический маятник, чтобы его частота колебаний была равна частоте колебаний пружинного маятника? Период колебания пружинного маятника вычисляется по формуле

Задание 878.

Как изменится период и частота колебаний упругой доски, установленной на вышке для прыжков в воду, если после взрослого человека на доске раскачивается мальчик, готовясь к прыжку?

Задание 879.

Когда груз неподвижно висел на вертикальной пружине, ее удлинение было равно 5 см. Затем груз оттянули вниз и отпустили, вследствие чего он начал колебаться. Каков период колебания?

Задание 880.

Шарик с отверстием, прикрепленный к легкой пружине жесткостью 250 Н/м, может совершать незатухающие колебания вдоль стержня в горизонтальном направлении (рис. 248). Чему равно ускорение, испытываемое шариком в положении равновесия и в крайних положениях, если амплитуда колебаний равна 4 см, а масса 50 г?

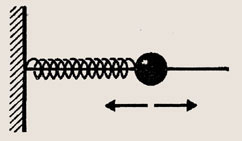
Рис. 248

Задание 881.

Опишите превращения механической энергии, совершающиеся в процессе свободных незатухающих колебаний пружинного маятника в горизонтальном направлении; в вертикальном направлении. Сохраняется ли полная механическая энергия в процессе колебаний?

Задание 882.

Груз массой 400 г совершает колебания на пружине жесткостью 250 Н/м. Амплитуда колебаний равна 15 см. Чему равны полная механическая энергия колебаний и наибольшая скорость движения груза?

Задание 883.

По условию задачи 880 определите полную энергию колебаний шарика, а также потенциальную и кинетическую энергии в тот момент, когда шарик находится в точке с координатой х = 2 см. За начало отсчета примите положение равновесия шарика.

Задание 884.

Груз, подвешенный на пружине жесткостью 1 кН/м, колеблется с амплитудой 2 см. Найдите кинетическую и потенциальную энергии при фазе

Задание 885.

Почему легче идти в обуви на толстой упругой подошве при определенной частоте шагов? Объясните с точки зрения превращения энергии.

Задание 886.

Как изменяется амплитуда и какие превращения претерпевает энергия при колебаниях дерева при одиночном порыве ветра, автомобиля при работе двигателя на холостом ходу, коромысла весов при взвешивании?

Задание 887.

Вода, которую мальчик несет в ведре, начинает сильно расплескиваться. Мальчик меняет темп ходьбы или просто «сбивает ногу», и расплескивание прекращается. Почему так происходит?

Задание 888.

Максимальную амплитуду вертикальных колебаний мячика, подвешенного на тонкой резинке, можно получить, если его нести и за 1 мин делать 48 шагов. Определите коэффициент упругости резинки, если масса мячика равна 60 г.